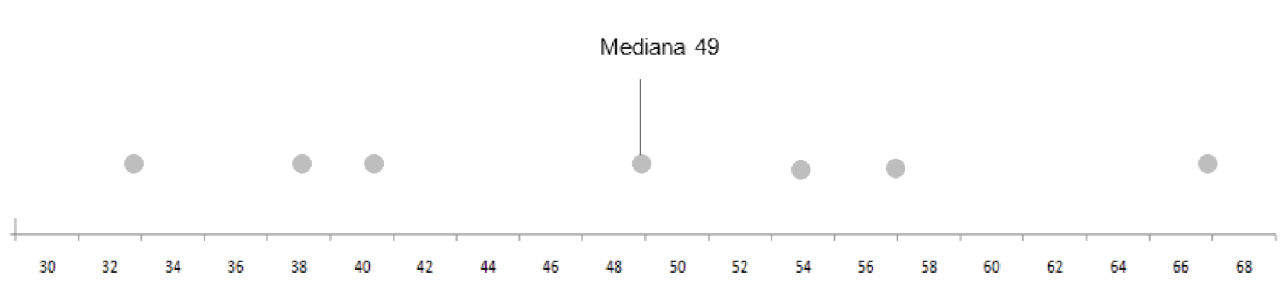
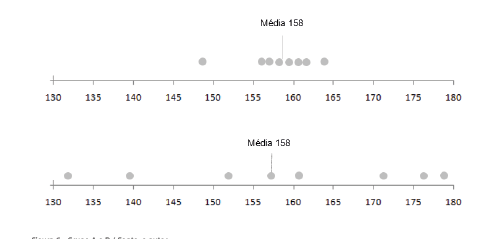
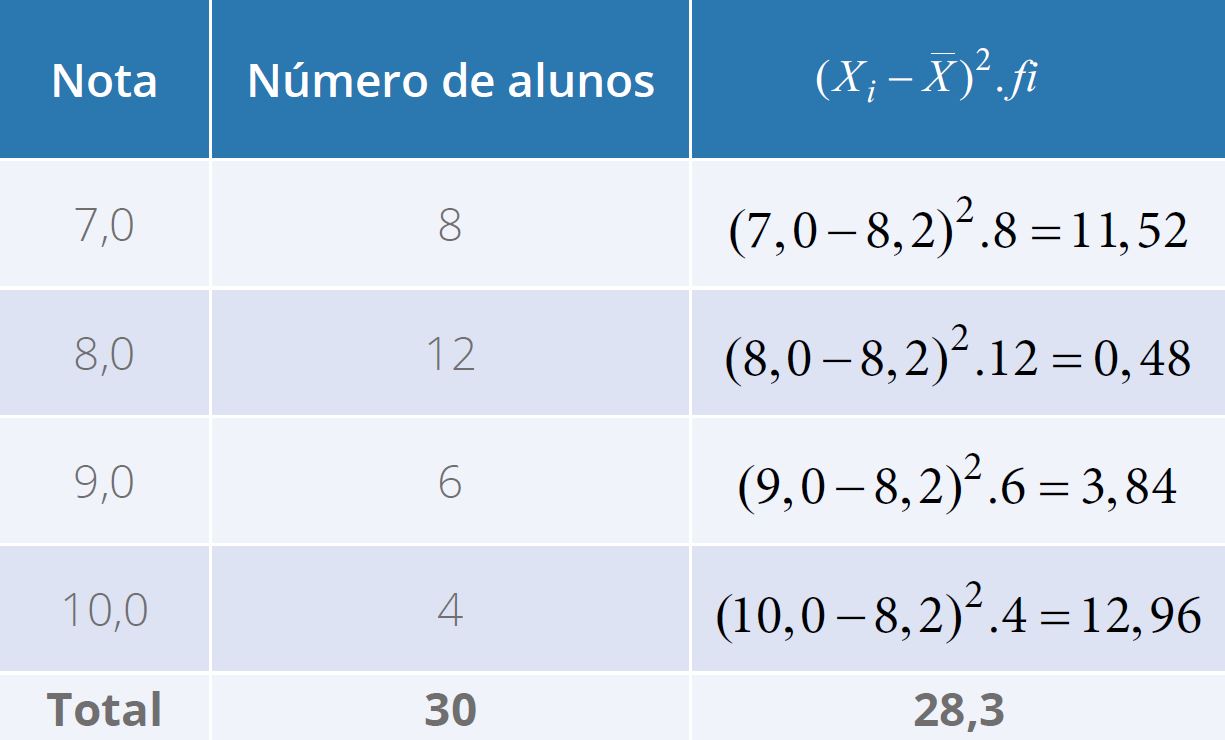
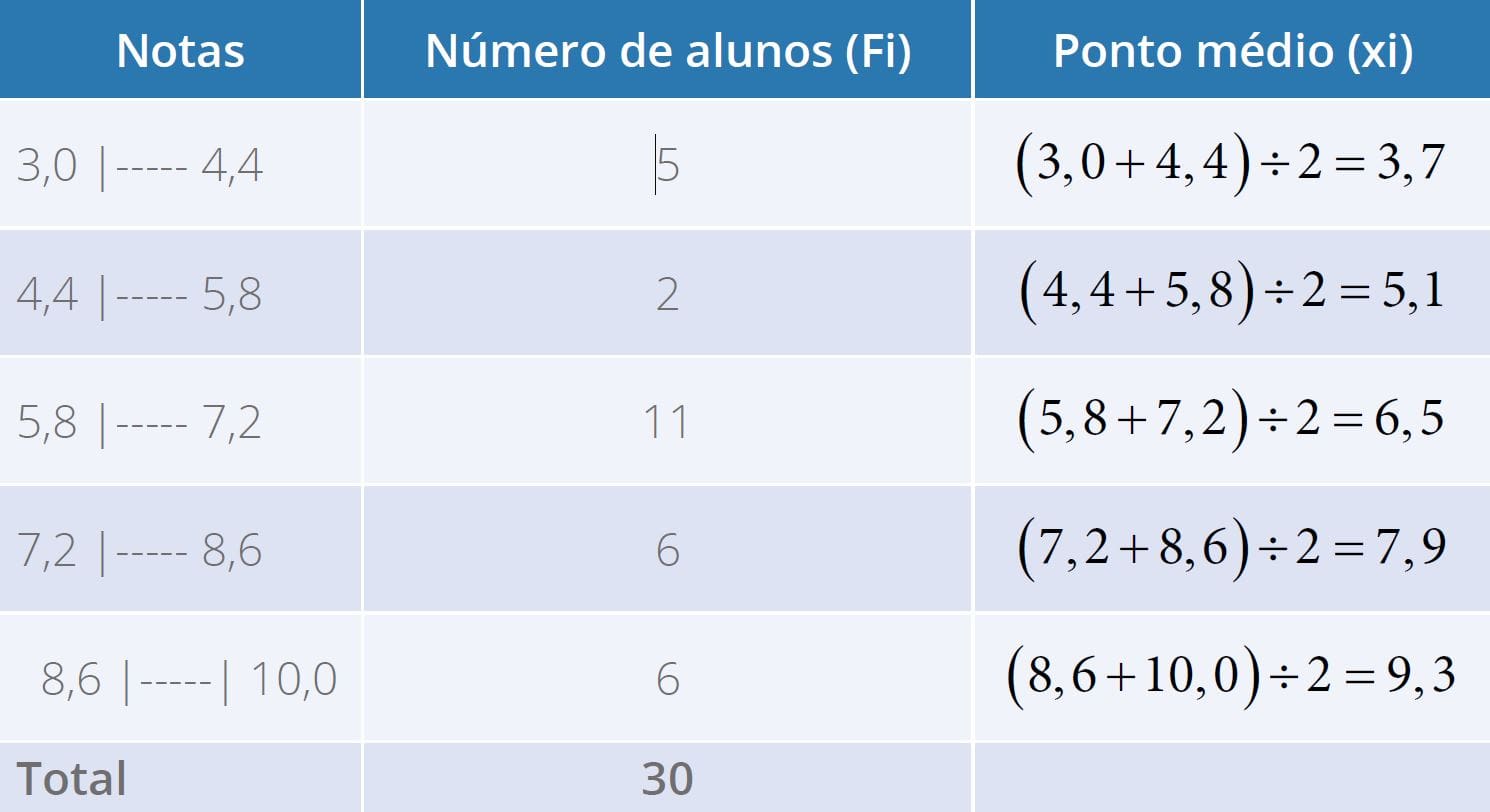
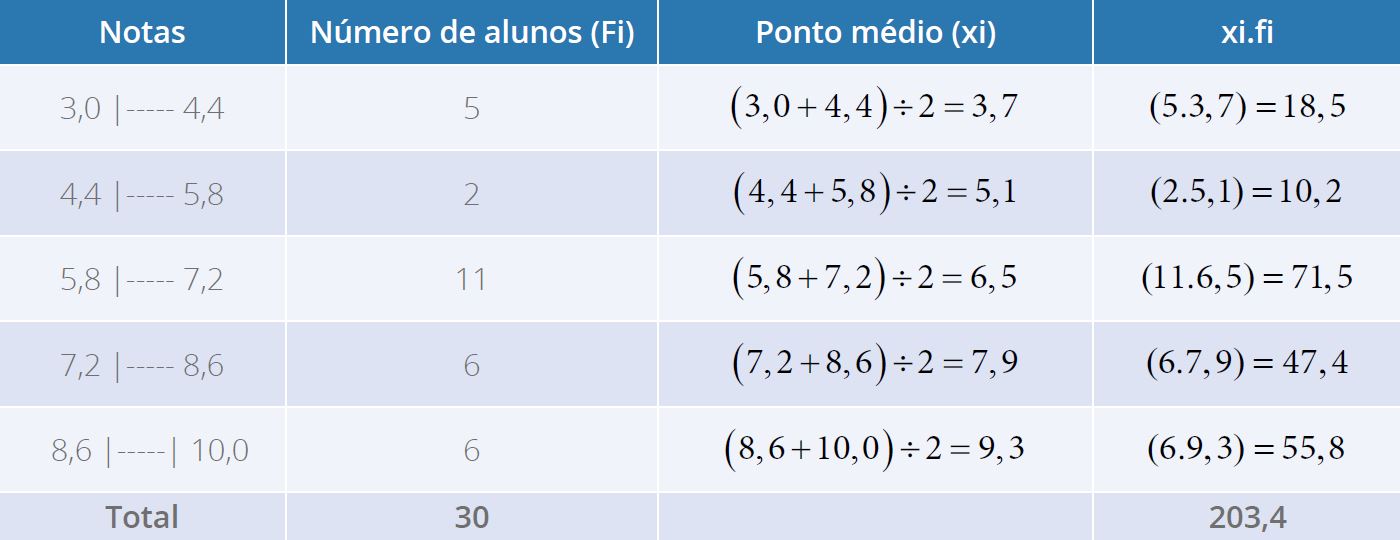
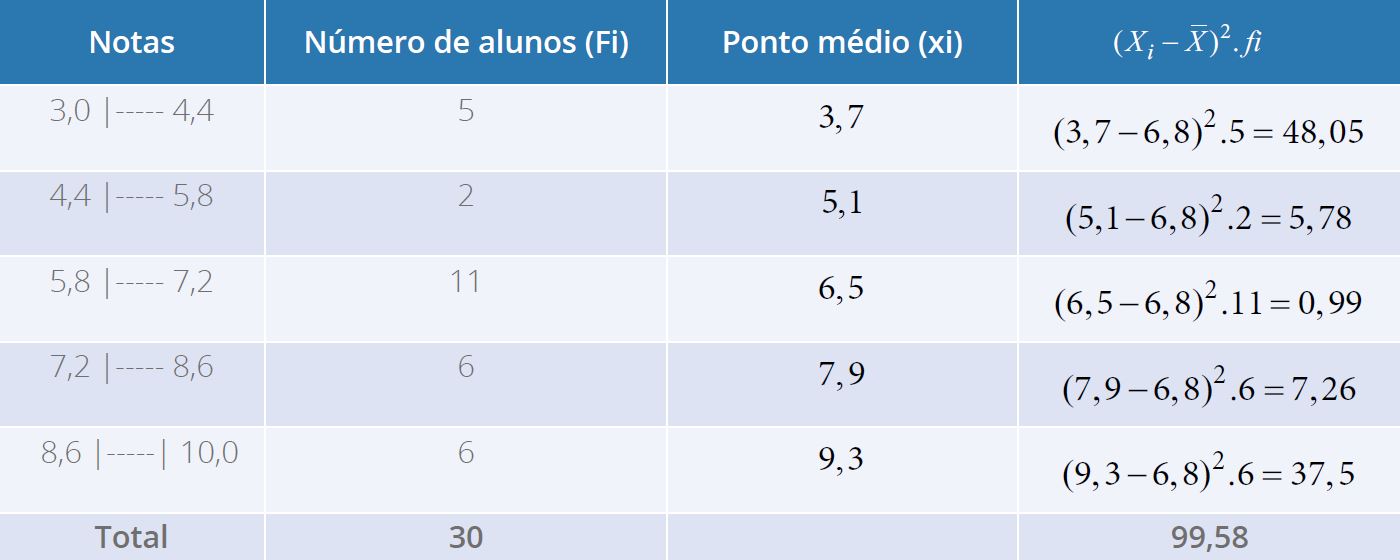
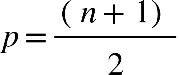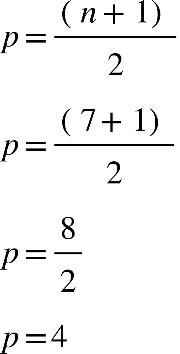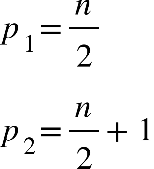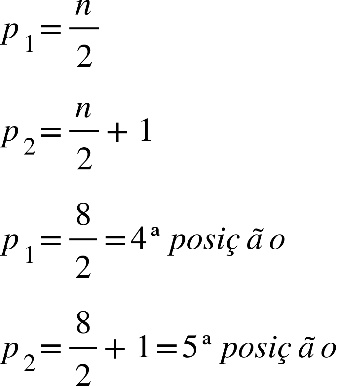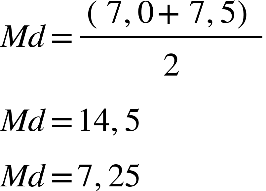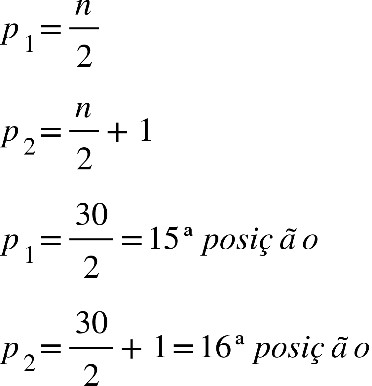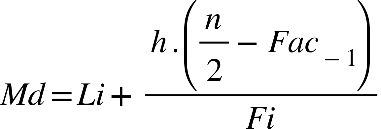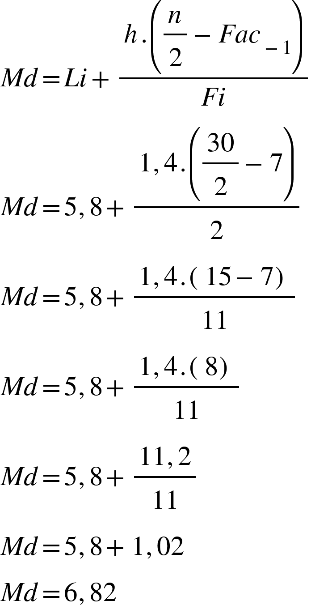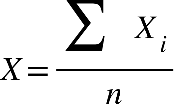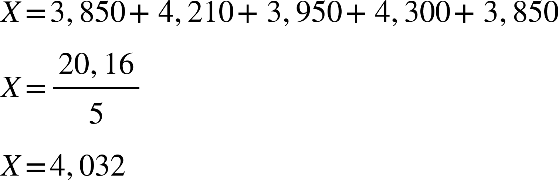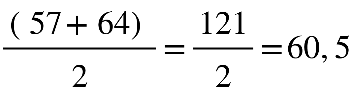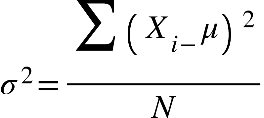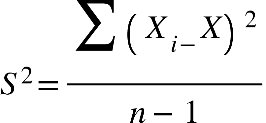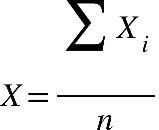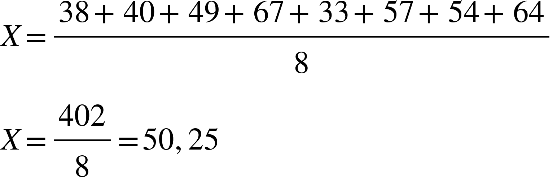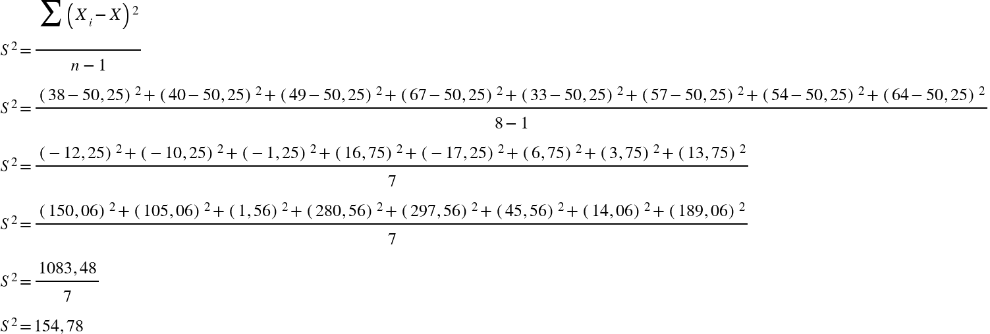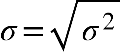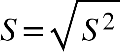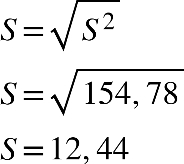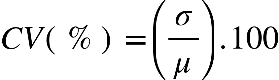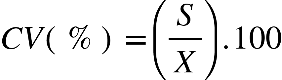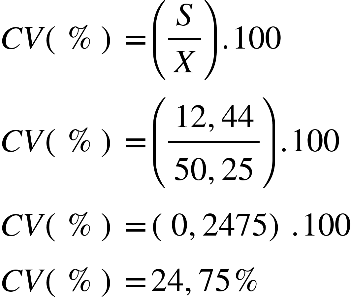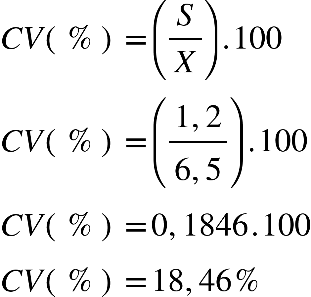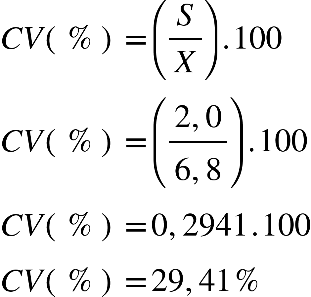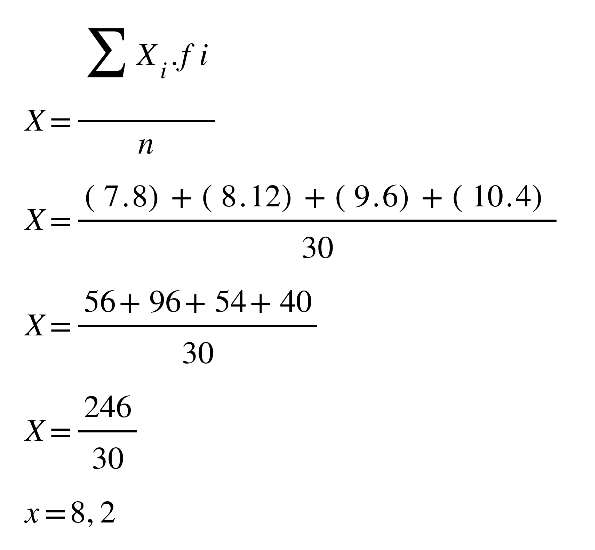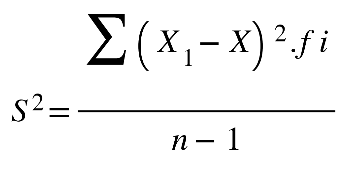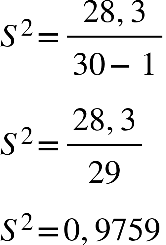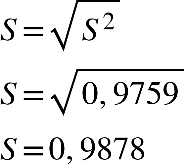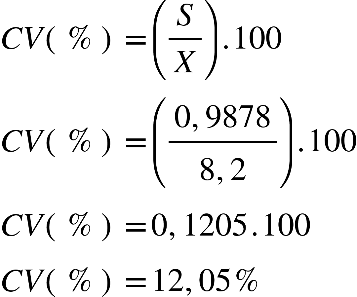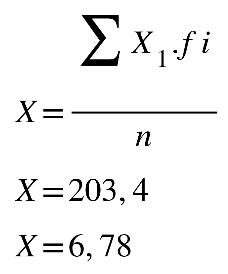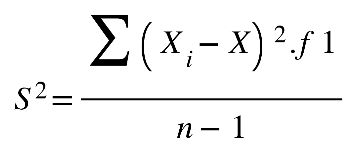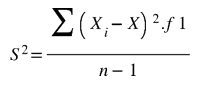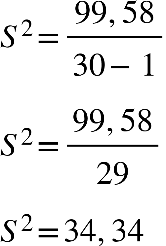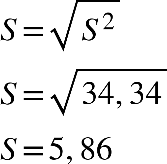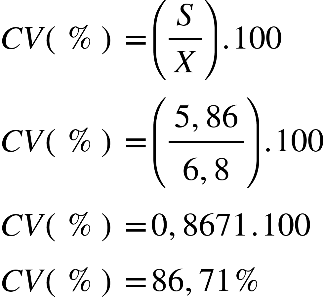Fonte: Parenti, Silva e Silveira (2017, p. 120).
A medida de tendência central mais conhecida e mais
utilizada é a média, mas não é sempre que ela é a mais
apropriada para representar os dados, às vezes, a mediana
é mais adequada para representar um conjunto de dados.
Isso ocorre sempre que a variabilidade dos dados for alta,
pois a média é afetada por valores extremos, e a mediana
não, ela apenas leva em consideração os valores centrais.
Outra medida de posição importante é a
moda
. Você deve ter ouvido falar da expressão: “música que está na
moda”, “roupa que está na moda”, isso significa que tem muita
frequência, muitas pessoas ouvindo a mesma música, muitas
pessoas usando mesmo estilo de roupa. Aqui na Bioestatística,
esse conceito é bem válido. Assim, para Martinez (2015), a
moda é a observação que ocorre com maior frequência no
conjunto de dados, ou seja, o valor que mais se repete.
Imagine que em uma loja de calçados femininos foram vendidos
20 pares de sapatos em um único dia. Os pares tinham estas
numerações:
|
34
|
37
|
34
|
36
|
36
|
|
35
|
36
|
37
|
33
|
36
|
|
36
|
36
|
36
|
36
|
39
|
|
36
|
35
|
34
|
36
|
36
|
A numeração que aparece com mais frequência é o número 36.
Significa que é uma informação muito importante ao gerente da
loja, pois indica que ele não pode deixar de ter calçados 36
em seu estoque, porque vendem com mais frequência.
É importante não confundir moda com maioria. A moda é a
observação mais frequente, mas isso não implica,
necessariamente, que a moda corresponde à maioria das
observações. (E. Z. Martines).Em outro exemplo, suponha que,
em uma turma de 1º ano de Nutrição, as idades dos 20 alunos
(em anos completos) são:
|
30
|
25
|
19
|
18
|
18
|
|
18
|
18
|
18
|
18
|
18
|
|
19
|
20
|
23
|
25
|
27
|
|
24
|
22
|
22
|
18
|
18
|
Podemos descrever, adequadamente, as idades destes alunos
dizendo que a idade mais frequente, ou moda, é 18 anos. No
entanto, em alguns casos, a moda pode não ser a medida mais
apropriada para caracterizar os dados. Como os valores a
seguir são os níveis séricos de triglicérides (em mg/dl) em
uma amostra de sete pacientes:
189, 72, 109, 140, 140, 140, 135
A moda, neste exemplo, seria 140 mg/dl, sendo o valor mais
frequente. Mas será que a moda é a medida de posição que
melhor caracteriza esses dados? Talvez a média ou a mediana
(que veremos a seguir) sejam mais úteis para esta finalidade.
Em algumas situações, a moda pode não ser única. Por exemplo,
o tempo de aleitamento materno (em meses) de 8 crianças
usuárias de um serviço de saúde:
1, 2, 3, 3, 4, 6, 6
Neste exemplo, temos dois valores mais frequentes, 3 e 6
meses. Podemos dizer que se trata de uma série bimodal, ou
seja, dois valores de moda. Novamente, a média ou a mediana
podem ser mais úteis para descrever os dados desse exemplo.
Podemos não ter moda em um conjunto de dados, caso nenhum
número se repita mais vezes do que outro. Quando isso
acontece, chamamos a distribuição de amodal. Se tivermos mais
do que duas modas, teremos uma distribuição multimodal
(PARENTI; SILVA; SILVEIRA, 2017).
Em alguns casos podemos ter interesse em saber a moda, mas os
dados estão apresentados em tabela, como fazer? Bem simples,
basta olharmos os dados e a coluna frequência, assim, vamos
encontrar a classe modal, para então sabermos a moda. Observe
os dados a seguir, na Tabela 8.
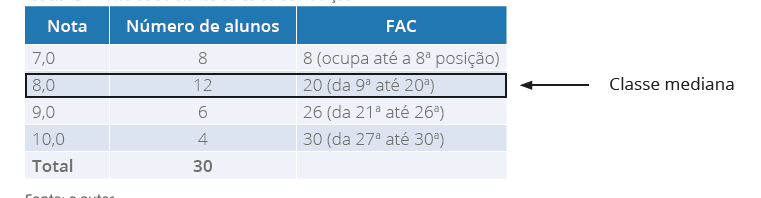
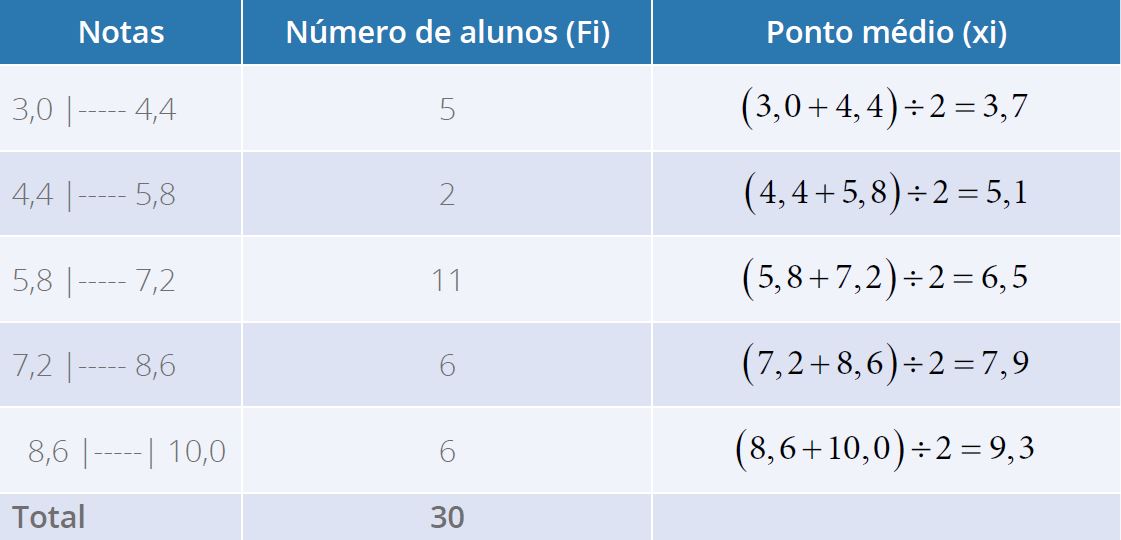
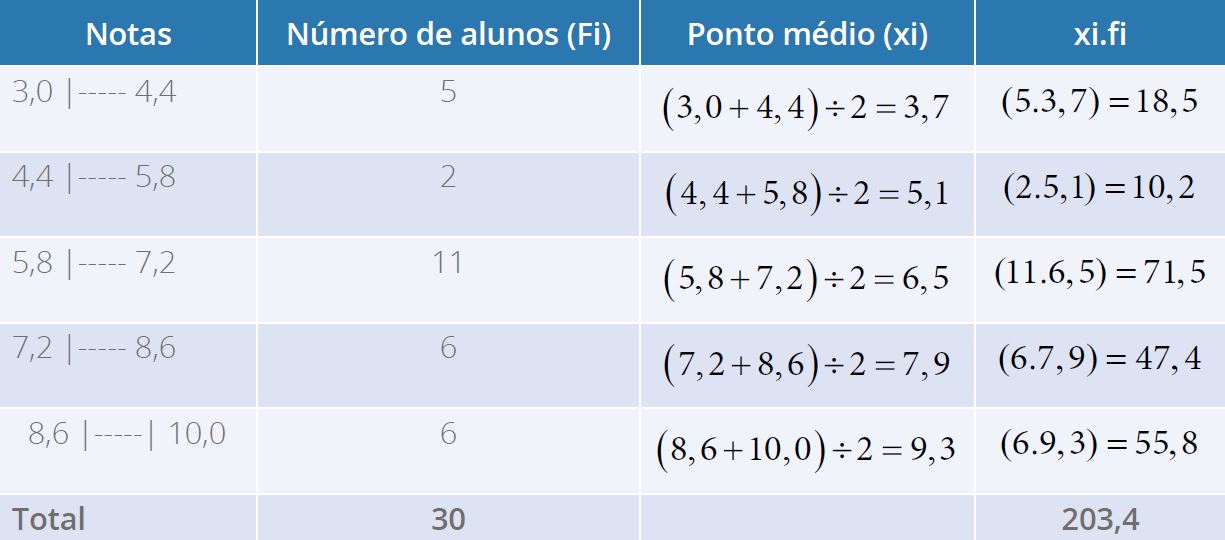
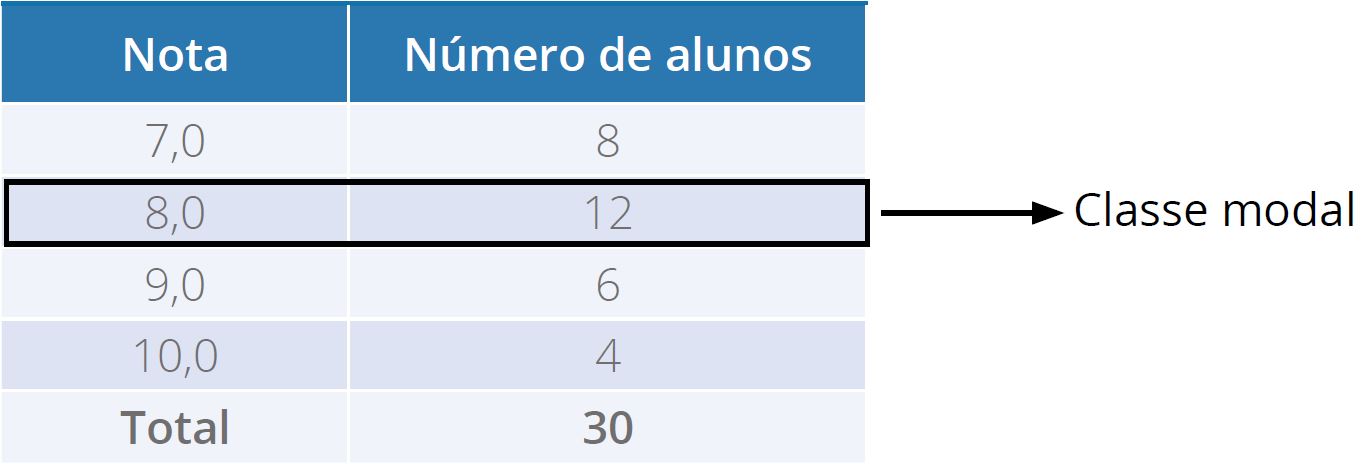
Tabela 8 - Notas de alunos do Curso de Nutrição
Fonte: a autora
Para determinar a moda em tabelas, primeiramente,
procuraremos a
classe modal
. Para isso, basta observar na coluna que tem a maior
frequência. Em nosso exemplo, a segunda classe tem doze
alunos, que corresponde ao valor que aparece com mais
frequência, portanto, esta é a classe modal.
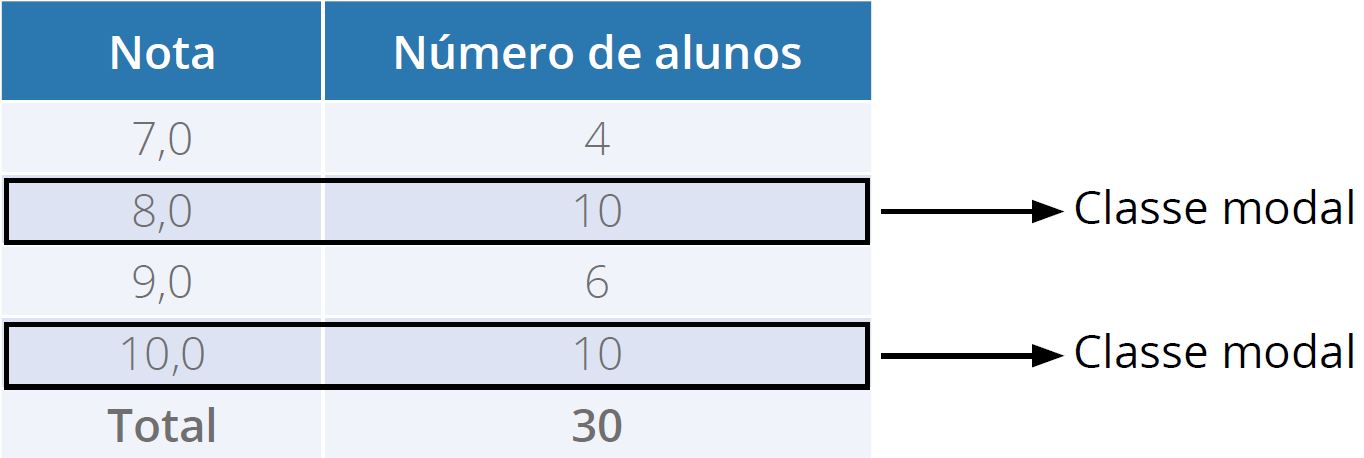
Em tabelas de frequências, também, podemos ter mais do que uma
moda. Analise a seguir, na Tabela 9.
Tabela 9 - Notas de alunos do Curso de Nutrição
Fonte: a autora.
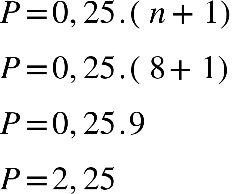
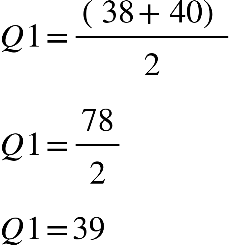







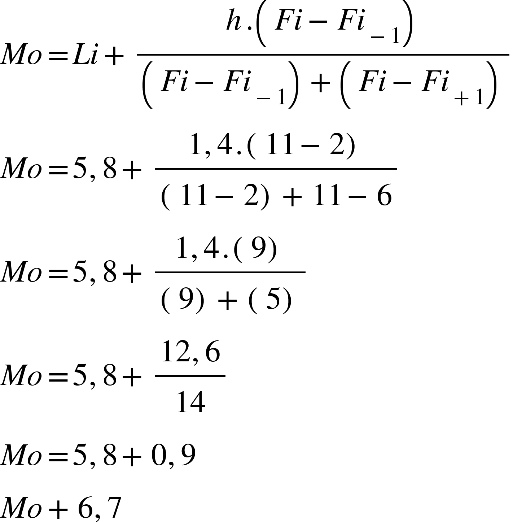
.png)