Assim, convido você a fazer um levantamento de artigos, reportagens, que tragam situações envolvendo correlação linear, regressão linear e inferência estatística. Faça um compilado e comece a identificar que os testes de hipóteses poderão ajudá-lo na tomada de decisões.

Desenvolva seu potencial

Agora,  avaliaremos se há uma associação entre duas variáveis com características quantitativas, que é objetivo de inúmeros estudos em ciências biológicas e/ou da saúde. Por exemplo: um biomédico pode ter interesse se há relação entre a quantidade de chumbo em medida na água e no volume de efluentes despejados em certo rio; um profissional da área da saúde pode querer saber se existe relação entre a pressão arterial e idade das pessoas; um professor pode querer saber a relação entre peso e altura, e assim por diante.

Quando existe a necessidade de analisar a relação entre essas duas variáveis, chamamos de correlação.

Vejamos um exemplo: um professor de enfermagem deseja saber se existe correlação entre o tempo dedicado ao estudo e o desempenho dos alunos na disciplina Bioestatística. Assim, ele selecionou oito alunos, assim, podemos observar o número de horas (x) e nota obtida na prova de Bioestatística (y) para cada aluno(a).

Tabela 1 - Relação entre as horas de estudo e nota na disciplina de Bioestatística

Fonte: o autor

Para analisarmos se há correlação entre as variáveis X e Y, inicialmente, os dados são representados em um gráfico cartesiano de pontos, que chamamos de diagrama de dispersão. Cada ponto do gráfico corresponde a um aluno e é marcado segundo seu valor para X e para Y (Figura 1).

Figura 1 - Gráfico de dispersão sobre a relação entre horas de estudo (X) e nota na disciplina de bioestatística (y)

Fonte: o autor.

Analisando a Figura 1, podemos observar que os alunos que se dedicaram estudando por mais horas tiveram um desempenho melhor, e os que dedicaram menos horas ao estudo, a ter um desempenho pior na prova. Entretanto podemos observar que temos algumas exceções, como o aluno “C” que se dedicou horas de estudo e sua nota foi 4. Isso significa que, embora pareça existir uma correlação entre estas duas variáveis, ela não é perfeita.

Para sabermos com mais precisão, existe outra maneira, que é avaliar a correlação e usar um coeficiente, que tem a vantagem de ser um valor numérico.

O coeficiente de correlação produto-momento (r) é uma medida da intensidade de associação existente entre duas variáveis quantitativas, e sua fórmula de cálculo foi proposta por Karl Pearson em 1896. Por essa razão, é também denominado coeficiente de correlação de Pearson. Por ter sido o primeiro a ser proposto (vários outros foram criados depois), muitas vezes r recebe simplesmente nome de coeficiente de correlação (MARTINEZ, 2015, p. 85).

O coeficiente de correlação pode variar entre -1 e +1. Quando temos valores negativos de r, temos correlação do tipo inversa, ou seja, à medida que X aumenta Y diminui. Já quando temos valores positivos para r ocorrem quando a correlação é direta, ou seja, X e Y variam no mesmo sentido. Por exemplo, temos que as taxas sanguíneas de insulina e glicose apresentam correlação negativa; enquanto a taxa do hormônio glucagônio tem correlação positiva com a glicemia (MARTINEZ, 2015).

É importante salientar que, quando temos uma correlação linear negativa, não significa que é uma correlação ruim , apenas o sentido do gráfico será decrescente. O valor máximo (tanto r = +1 como r = -1) é obtido quando todos os pontos do diagrama estão em uma linha reta inclinada. Quando temos uma correlação linear igual a r +1, significa que temos uma correlação linear perfeita e positiva, como você pode observar na Figura 2.

Figura 2 - Correlação quando r = +1 / Fonte: o autor.

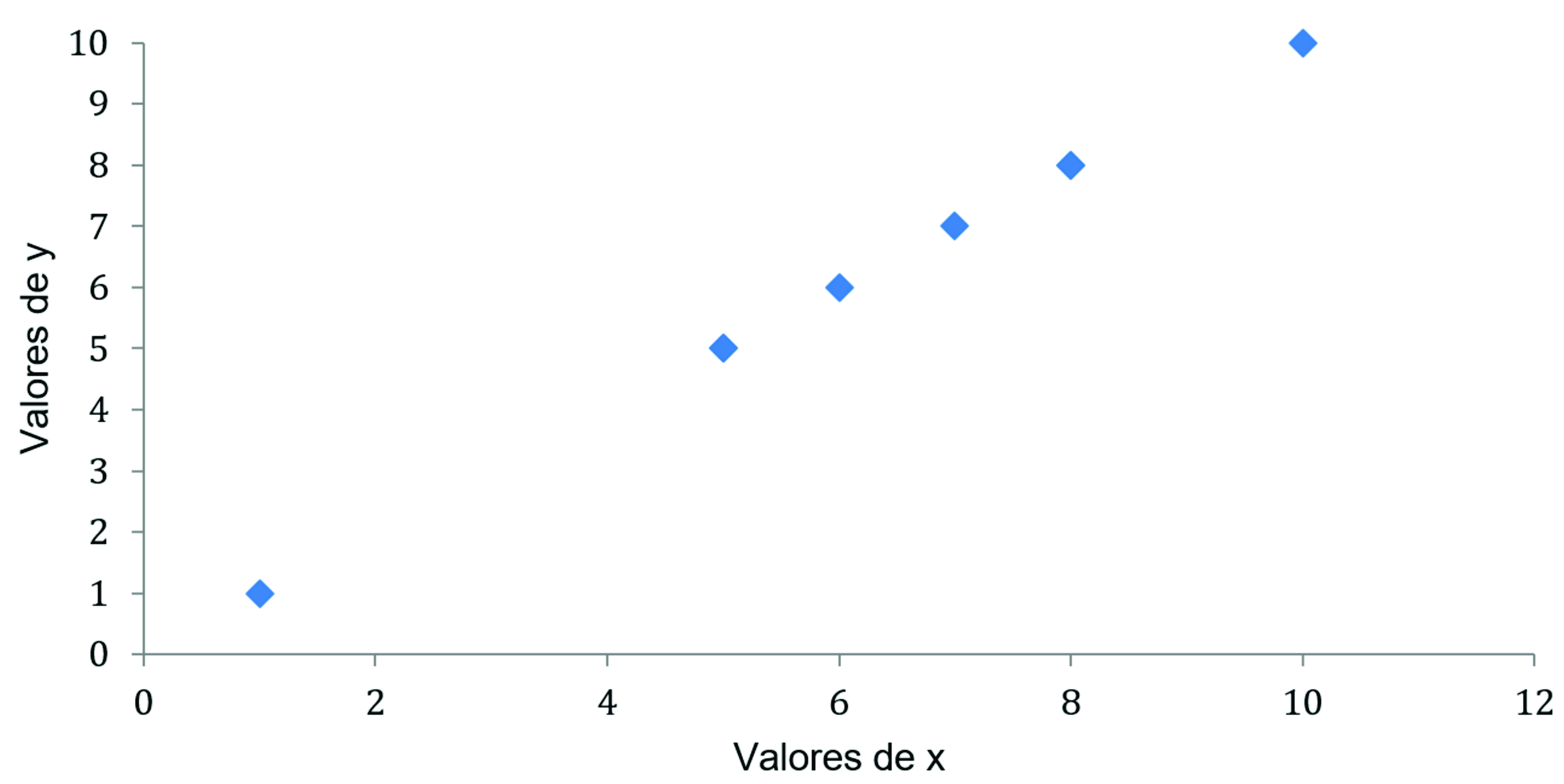
Quando temos uma correlação linear igual r -1, significa que temos uma correlação linear perfeita e negativa, como você pode observar na Figura 3.

Figura 3 - Correlação quando r = -1 / Fonte: o autor.

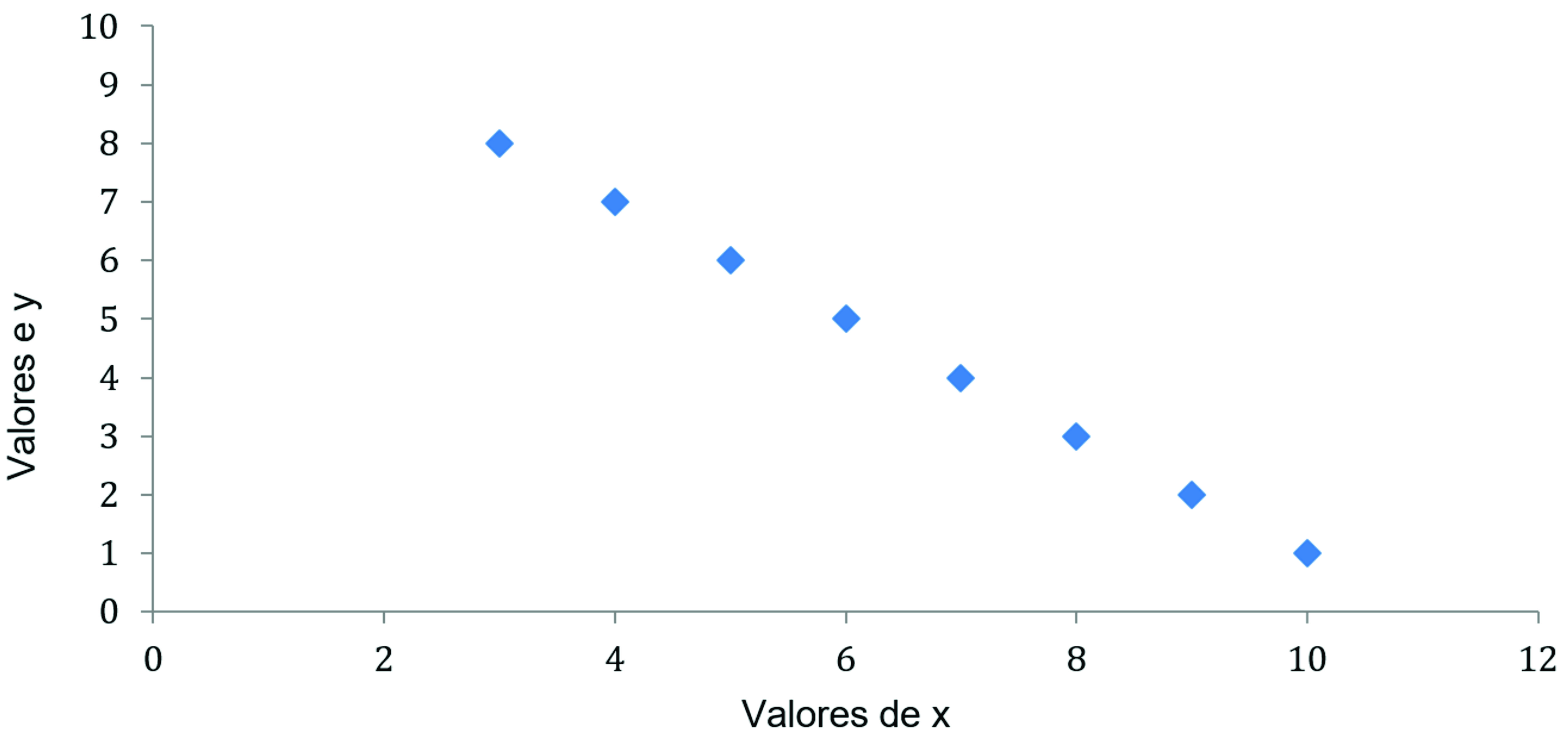
Por outro lado, quando não existe correlação entre X e Y, os pontos se distribuem de maneira que não temos uma relação, podendo ser em formato de nuvens circulares ou formatos não definidos, não tendo uma tendência crescente ou decrescente (Figura 4).

Figura 4 - Correlação quando r = 0,09 / Fonte: o autor.

As associações (X e Y) de grau intermediário (r entre 0 e |1|) apresentam-se como nuvens inclinadas, de forma elíptica, como podemos observar na Figura 5.

Figura 5 - Correlação quando r = 0,65 / Fonte: o autor.

O que significa, então, esses valores de r? Observe a Figura 6 a seguir, que traz uma correlação igual a r = 0,56.

Figura 6 - Correlação quando r = 0,55 / Fonte: o autor.

Segundo Zou et al. (2003) a proposta para interpretação do coeficiente de correlação linear (r) pode ser observada no Quadro 1.

Quadro 1 - Interpretação do coeficiente de correlação linear

Fonte: adaptado de Zou et al . (2003).

Zou et al . (2003) interpretam o sinal do coeficiente de correlação como a direção da associação. Os coeficientes de correlação linear que são maiores do que zero apresentam correlações positivas (quanto maior X, maior Y), e coeficientes menores que zero indicam correlações negativas (quanto maior X, menor Y) . Já a correlação igual a zero indica que não existe uma correlação linear.

É importante salientar que a interpretação de r pode variar de acordo com a experiência de autores, principalmente as intermediárias (-0,8, 0,5, -0,2, -0,3 e outros), o que não muda é que +1 e -1 são correlações perfeitas e zero não há correlação linear. Para facilitar nosso entendimento, analise na Figura 7 que quanto mais próximo aos extremos (-1 e +1) mais forte é a correlação, e, à medida que se aproxima de zero, a correlação vai ficando mais fraca.

Figura 7 - Correlação quando r = 0,55 / Fonte: o autor.

Agora que temos a equação que determina o coeficiente de Pearson, vimos que se trata de uma equação bem complexa, mas fique tranquilo(a), querido(a) aluno(a), resolveremos juntos o passo a passo. Vejamos um exemplo: um professor de ciências biológicas deseja saber se existe correlação entre o tempo dedicado ao estudo e o desempenho dos alunos na disciplina de Bioestatística. Assim, ele selecionou oito alunos, assim, podemos observar o número de horas (X) e a nota obtida na prova de Bioestatística (Y) para cada aluno.

Tabela 2 - Relação entre as horas de estudo e nota na disciplina de Bioestatística

Fonte: o autor.

Para facilitar nosso cálculo, você deve ter percebido que vamos precisar elevar todos os valores de X ao quadrado, todos os valores de Y ao quadrado e somar tudo isso, então, vamos reescrever a tabela, com essas colunas. Observe a seguir (Tabela 3):

Tabela 3 - Relação entre as horas de estudo e nota na disciplina de Bioestatística

Fonte: o autor.

Quando falamos em relações lineares entre as variáveis X e Y, significa que, ao utilizarmos o coeficiente de correlação de Pearson, estamos nos referindo a uma situação em que uma variável é, direta ou inversamente, proporcional a outra (CRESPO, 2009). Vimos em nosso exemplo, que quanto às horas dedicadas a estudos tem uma relação forte com a nota da disciplina de Bioestatística.

Portanto, é de fundamental importância construir um gráfico de dispersão entre as variáveis antes de calcularmos o coeficiente de correlação (que já fizemos anteriormente, na Figura 7), e, então, observarmos se é realmente adequado utilizarmos essa medida de associação.

Figura 8 - Gráfico de dispersão sobre a relação entre horas de estudo (X) e nota na disciplina de Bioestatística (Y) / Fonte: o autor.

A resposta a esta pergunta não é simples. Em nenhuma situação podemos eliminar observações de nosso banco de dados com o propósito de deixar os resultados mais interessantes ou de destacar possíveis associações entre as variáveis que valorizariam nosso estudo, principalmente nas áreas biológica e da saúde, que podem trazer dados que podem orientar o direcionamento de uma pesquisa, além de não ser uma conduta ética por parte do pesquisador. Para isso, é importante que você vá novamente aos dados coletados, faça comparação com os dados da pesquisa de campo, verifique os questionários, os prontuários, a fonte original dos dados para, então, verificar a possibilidade de erros de digitação ou anotação. Ainda que não fosse esse o erro encontrado, não é correto eliminá-lo, arbitrariamente. É de suma importância buscar outras informações sobre aquele dado para possa entender se realmente ele pertence àquela população de interesse do estudo.

Depois que calculamos a correlação linear, podemos ter o interesse em determinar a Regressão Linear . A análise de regressão explicita em uma equação matemática a forma da relação entre uma variável chamada dependente e uma ou mais variáveis chamadas independentes , ou seja, quando temos o interesse, estudo da regressão aplica-se à quelas situações em que há razões para supor uma relação de causa-efeito entre duas variáveis quantitativas e se deseja expressar, matematicamente, essa relação.

O termo regressão deve-se a Francis Galton, que publicou, em 1886, um artigo no qual tentou explicar por que pais de alta estatura tinham filhos com estatura em média mais baixa do que a deles e pais de baixa estatura tinham filhos em média mais altos. Esse fenômeno foi chamado de regressão à média, termo que, apesar de inadequado para expressar a dependência entre duas variáveis quantitativas, acabou sendo incorporado pelo uso à linguagem estatística (MARTINEZ, 2015, p. 103).

Agora que já sabemos como determinar a correlação linear, relembraremos nosso exemplo: um professor de Enfermagem deseja saber se existe correlação entre o tempo dedicado ao estudo e o desempenho dos alunos na disciplina Bioestatística. Assim, ele selecionou oito alunos, assim, podemos observar o número de horas (X) e a nota obtida na prova de Bioestatística (Y) para cada aluno (apresentaremos a tabela a seguir, com as colunas necessárias para calcular a regressão linear).

Tabela 4 - Relação entre as horas de estudo e nota na disciplina de Bioestatística

Fonte: o autor.

Com a equação da reta, podemos substituir dois pontos quaisquer por X para traçar a reta. A Figura 9 apresenta-nos o gráfico de dispersão com a reta de regressão linear.

Figura 9 - Gráfico de dispersão e reta de regressão linear sobre a relação entre horas de estudo (x) e nota na disciplina de bioestatística / Fonte: o autor.

Podemos observar como o valor de r encontrado, anteriormente, foi igual a 0,80, e o valor de “bx” é positivo, nossa reta ajustada tem sentido crescente. Caso nosso valor de r fosse negativo, nossa reta ajustada teria o sentido decrescente. Outro ponto importante em uma análise utilizando ferramentas estatísticas é a inferência. Imagine que um profissional da saúde trabalha em um laboratório e está conduzindo um estudo cujo objetivo é analisar se um novo medicamento pode ser capaz de trazer bons resultados ao tratamento de determinada doença . Para realizar essa pesquisa, este profissional selecionou uma amostra de 80 pessoas portadoras da doença, e estas foram divididas em dois grupos com 40 pessoas cada. As pessoas do grupo A foram submetidas ao medicamento que está sendo avaliado, as pessoas do grupo B, receberam um placebo . Os resultados estão apresentados na Tabela a seguir:

Tabela 5 - Resultados do estudo

Fonte: o autor.

Podemos observar que: 20 4050 % das pessoas que estão no grupo A, responderam ao tratamento que está sendo avaliado, já 10 4025% das pessoas alocadas no grupo B responderam ao tratamento com o medicamento sem o princípio ativo (placebo). Dessa maneira, a razão entre essas porcentagens é 50252 %() / %() grupoAgrupoB = , isto é, podemos concluir que entre as 80 pessoas que tem a doença e estão participando do estudo, se utilizarem o medicamento (da pesquisa) tem o dobro de chances de responder à doença quando comparados ao grupo B.

Inicialmente, o resultado obtido descreve apenas as 80 pessoas que compuseram esta amostra. No entanto nosso intuito é que os nossos resultados tragam valor para todas as pessoas que fazem parte da população e que tenham essa doença, não importando se foram selecionados, ou não, para compor a amostra da pesquisa. Para obtermos isso, fazemos uso da inferência estatística , ferramenta usada para extrapolar os achados de nossa amostra para todos os indivíduos que fazem parte da população (MARTINEZ, 2015).

A Figura 10 apresenta-nos o processo pelo qual obtemos conclusões sobre uma população (N) a partir de dados obtidos, por meio de uma amostra (n).

Figura 10 - Representação de uma inferência estatística / Fonte: o autor.

Para estudarmos a inferência estatística, relembraremos alguns conceitos já estudados anteriormente (CRESPO, 2009):

Outro conceito importante que precisamos estudar aqui na inferência estatística é o Parâmetro , essencial para entendermos a inferência estatística. Trata-se de valor calculado a partir de uma população, ou seja, usando todos os elementos (MARTINEZ, 2015). Por exemplo: um professor de Farmácia quer estudar a altura (em cm) das crianças que estão cursando a 1ª série em determinado município. A população inclui todas as crianças deste município. A média da altura encontrada (em cm), que é calculada a partir da análise do peso de todas as crianças da população é um parâmetro.

Pedimos que tome cuidado para não confundir Parâmetro com Variável. O parâmetro, como já vimos, é uma característica numérica de uma população, já uma variável é uma característica dos indivíduos que estamos pesquisamos. Segundo Parenti, Silva e Silveira (2017), o parâmetro é um número fixo, já os valores de uma variável são passíveis de variação de um indivíduo a outro. Por exemplo: entre os alunos estudados, a idade e o prato preferido são variáveis , já a média da altura de todos os alunos de determinada cidade é um parâmetro .

A diferença entre uma média populacional (parâmetro) da média amostral (estimativa) é denotada por:
a) média populacional: representado pela letra grega μ.
b) média amostral: representado por “xis barra” X .

Assim, as principais ferramentas da inferência estatística são os intervalos de confiança e os testes de hipóteses. Podemos utilizar da seguinte forma:

A distância que temos entre a média e o limite do intervalo de confiança é exatamente igual à margem de erro. É importante salientar que o nível de confiança deve ser selecionado, previamente, pelo pesquisador, e que a média populacional fica dentro do intervalo de confiança .

Para calcular o limite superior XLS e inferior XLI do intervalo de confiança para nível de confiança igual a (1 – α) usa-se a seguinte expressão oriunda da discussão sobre as áreas embaixo da curva normal e a distribuição normal padronizada:

Em que:

X = média

Zc = Z crítico - valor a ser encontrado na Tabela de Curva Normal (Tabela Z)

S = desvio padrão

n = número de elementos da amostra

α = intervalo de confiança (ex.: 90%, 95%, 98%).

Figura 11 - Curva de Gauss

Fonte: o autor.

Tabela 6 - Tabela de distribuição Normal Reduzida

Fonte: Crespo (2009, p. 218). Encontramos o valor de 1,96. Você poderá encontrar qualquer valor utilizando somente a tabela Z.

Figura 12 - Representação do teste bicaudal para Tabela t student / Fonte: o autor.

Para resolver nosso exercício, temos que encontrar nosso tcrítico, assim, temos:

• 95% é nosso intervalo de confiança.
• Como nossa área interessada para trabalhar com essa tabela são as caudas , devemos encontrar esse valor.
• Se a área é 95%, para termos os 100%, faltam 5%, certo. São esses 5% que são divididos nas caudas.

Veja a Figura 13.

Figura 13 - Representação do teste bicaudal para Tabela t student / Fonte: o autor.

Como você pode perceber, os 95% é o que temos em nosso exercício, e os 5% foram divididos nas duas áreas do gráfico, representando 2,5% em cada cauda. Mas, para utilizar a tabela t Student, consideraremos que 5% teste são bicaudal, e procuraremos esse valor na tabela. Apenas mais um detalhe, antes de ir à tabela, é importante que você entenda que o grau de liberdade é igual a n – 1, portanto, temos 10 elementos, para o grau de liberdade teremos: 10-1 = 9. Assim, buscaremos “9” quanto ao grau de liberdade.

Vamos procurar a linha 9 e a coluna 5% em nossa tabela T Student apresentada a seguir:

Tabela 7 - Tabela t de Student - Probabilidade para um teste bicaudal

Fonte: Barbeta et al. (2014, p. 300).

Assim o valor encontrado é igual a 2,2622, agora, resolveremos nosso exercício.

Uma hipótese estatística refere-se à suposição do parâmetro populacional, como:

São dois os tipos de hipóteses: designa-se H0, denominada hipótese nula, a hipótese estatística a ser testada, e H1, a hipótese alternativa. A hipótese nula expressa uma igualdade, enquanto a hipótese alternativa é dada por uma desigualdade.
São exemplos de hipóteses para um teste estatístico:

Existem dois tipos possíveis de erros quando fazemos um teste estatístico para aceitar ou rejeitar H0. Nós podemos rejeitar a hipótese H0, quando ela é verdadeira, ou aceitar H0, quando ela é falsa (MARTINEZ, 2015). O erro de rejeitar H0, sendo H0 verdadeira, é denominado Erro tipo I, e a probabilidade de se cometer o Erro tipo I é designada α. Por outro lado, o erro de aceitar H0, sendo H0 falsa, é denominado Erro tipo II, e a probabilidade de cometer o Erro tipo II é designada β.

Os possíveis erros e acertos de uma decisão com base em um teste de hipótese estatístico estão apresentados a seguir:

Dentro do teste de hipóteses, temos as regiões de aceitação e rejeição, a saber:

Teste bilateral

A região crítica está nas duas regiões extremas (caudas) sob a curva (Figura 14).

Figura 14 - Teste bilateral / Fonte: o autor.

Teste unilateral à direita

A região crítica está na região extrema (cauda) direita sob a curva (Figura 15).

Figura 15 - Teste unilateral à direita / Fonte: o autor.

Teste unilateral à esquerda

A região crítica está na região extrema (cauda) esquerda sob a curva (Figura 16).

Figura 16 - Teste unilateral à esquerda / Fonte: o autor.

Depois de apresentarmos os conceitos fundamentais dentro de um teste de hipótese, você verá que não é um teste complicado. A seguir, apresentaremos o roteiro para realização de um teste de hipóteses.

Os valores críticos de z relativos aos níveis de significância usados com maior frequência podem ser observados a seguir (valores já retirados da Tabela Z de distribuição normal reduzida):

Para entendermos este passo a passo, vejamos um exemplo: supondo que um professor de ciências biológicas deseja testar H0: μ = 20 contra H1: μ > 20, sabendo que o desvio padrão da população é igual a 4 e a amostra testada foi de 16 elementos:

Nesse caso, queremos obter o teste de hipóteses com uma média diferente de 50, certo? Então, utilizaremos o teste bilateral. Resolvendo o exercício passo a passo, temos:

Figura 18 - Teste bilateral / Fonte: o autor.

Novos desafios

Você percebeu, caro(a) estudante, que a correlação e a regressão linear poderão ajudá-lo(a) como professor(a). Você pode ter uma turma, analisar duas disciplinas e fazer projeções sobre as possíveis notas de seus alunos, desde que tenham uma correlação linear forte. Você, também, identificou como as técnicas estudadas em Bioestatística sobre a inferência poderão, por meio de testes, construir um modelo de aceitação ou rejeição de uma hipótese.

Espero que tenha tirado máximo proveito desse conteúdo.