TEMA DE APRENDIZAGEM
Tabelas e Gráficos em Bioestátistica e epidemiologia
Para começarmos a nossa jornada, compartilharei uma experiência profissional para que possamos problematizar e, consequentemente, refletir. A primeira vez que participei de uma pesquisa de campo foi para fazer um diagnóstico para elaboração de um Plano de Gerenciamento de Resíduos Sólidos (PGRS), em uma empresa de revenda de peças para automóveis. Para aproveitar ao máximo o tempo na empresa e a visita in loco , elaborei um check list bem simples que trazia informações sobre: tipo de resíduo, quantidade gerada (kg/mês) e como estava sendo feita a destinação final deste resíduo neste momento.
Depois de fazer a visita, coletar os dados, foi preciso trabalhar nesses dados, afinal, não poderia entregar à empresa o check list em que fiz a coleta de dados. Assim, a partir dos dados coletados, elaborei uma tabela bem organizada dentro das normas da ABNT e também fiz um gráfico apontando o resíduo que era gerado em maior quantidade, assim, poderia indicar o que meu cliente poderia fazer para cumprir a legislação e minimizar os custos que ele tinha com a destinação final de resíduos.
Assim, os gráficos e as tabelas são as principais formas de apresentação dos resultados de uma pesquisa. Conhecer as regras e as normas específicas que regem a construção de tabelas, além de aprender o passo a passo para sua construção é importante e imprescindível para a compreensão e, também, para orbitarmos neste universo estatístico e bioestatístico.
É importante, também, compreendermos, corretamente, como construir e interpretar gráficos. Podemos perceber que a Bioestatística pode ajudar com as regras e as etapas para a construção de uma tabela ou um gráfico. Sabemos que muitos alunos têm a dificuldade de lidar com tabelas e gráficos.
Para isso, convido você a fazer a leitura do artigo intitulado Análise e interpretação de tabelas e gráficos estatísticos . A fim de utilizar dados interdisciplinares. Nesse artigo, você verá o ensino e a aprendizagem da Estatística bem como a utilização de procedimentos e conceitos.
Os dados sobre a dengue, daremos continuidade no mesmo exemplo, tudo bem? Sabemos que esta nossa situação é hipotética, e você, graduando (a) na área de Biológicas e da Saúde, que está atuando em sala de aula, quer fazer um experimento a respeito dos casos de dengue do seu bairro. Desta forma, faça uma pesquisa em forma de formulário com dez pessoas, que podem ser membros de sua família ou mesmo colegas de trabalho, contendo a seguinte pergunta: Você já teve dengue? Com isso, as possíveis respostas do seu formulário serão: ( ) Sim ou ( ) Não.
Organize estes dados com a quantidade de pessoas que responderam sim e a quantidade de pessoas que responderam não . Em seguida, construa uma tabela ou um gráfico, mediante os resultados desta pesquisa e, ao fazê-lo, você já estará utilizando mais uma técnica apresentada pela bioestatística.
Uma apresentação tabular de dados é a representação das informações por intermédio de uma tabela. Uma tabela é um meio bastante eficiente de mostrar dados levantados, facilitando a sua compreensão e interpretação. Além disso, auxilia o entendimento global e o relacionamento entre as variáveis representadas.
Conheça as normas para apresentação dos dados em tabelas bem como definições, terminologia e simbologia: IBGE – Normas de apresentação tabular (IBGE, 1993). NBR 14724:2011 - Informação e documentação - Trabalhos acadêmicos – Apresentação (ABNT, 2011).
Na construção de tabelas, os dados são apresentados em colunas verticais e linhas horizontais, conforme a classificação dos resultados da pesquisa. Algumas orientações preliminares são as seguintes (ARANGO, 2011, p. 31):
Para construção de uma tabela é importante que ela seja: simples, clara e objetiva. Assim, é apropriado que grandes volumes de informação sejam descritos em várias tabelas, ao invés de serem apresentados em uma única tabela;
Uma tabela precisa ser auto-explicativa, ou seja, sua compreensão não deve ser vinculada do texto. Dessa forma, nenhuma “casa” da tabela deve ficar em branco, sempre apresentando um símbolo ou número, caso houver duas ou mais tabelas em um texto, deverão receber um número de identificação, que será referido no texto.
As colunas externas de uma tabela não devem ser fechadas.
Na parte superior e inferior, as tabelas devem ser fechadas por linhas horizontais.
A utilização de linhas verticais para separação de colunas no corpo da tabela é opcional.
Ao fazer arredondamentos de números, é importante que seja mantida uniformidade quanto ao número de casas decimais.
Os totais e os subtotais devem ser destacados, como por exemplo, em negrito.
A tabela deve ser maior no sentido vertical que no horizontal. Contudo, se uma tabela apresentar muitas linhas e poucas colunas (estreita demais), convém separá-la em uma maior quantidade de colunas. Neste caso, as colunas deverão ser separadas por linhas duplas.
Sendo assim, uma tabela pode ser dividida, hierarquicamente, em dois componentes chamados: principais e secundários. Os componentes principais são (ARANGO, 2011, p. 32):
referente ao conjunto das informações, dos dados que foram coletados e que aparecem no decorrer da tabela, no sentido horizontal e vertical.
é a divisão em sentido vertical, onde aparece a designação da natureza do conteúdo da linha.
indica a natureza do conteúdo de cada coluna.
refere-se as divisões que aparecem no corpo da tabela.
Segundo Arango (2011, p. 32), as partes secundárias compreendem:
Depois de compreendidas as partes secundárias, observaremos a simbologia comumente utilizada em tabelas estatísticas, como mostra o exemplo do Quadro 1 e seus significados.
Quadro 1 - Símbolos utilizados em tabelas estatísticas
Fonte: adaptado de Arango (2011).
Com essas informações, uma amostra representativa da população de domicílios deveria observar que:
Todo número inteiro constituído de mais de três algarismos deve ser agrupado de três em três, da direita para a esquerda, separando cada grupo por um ponto (p. ex.: 56.342.901).
Exceto:
I. Algarismos que representam o ano (p. ex.: 2010).
II. Números de telefone (p. ex.: 3222-2222).
III. Placas de veículos (p. ex.: AAA 2222).
A parte decimal de um número deverá ser separada da parte inteira pela vírgula (p. ex.: 0,56).
A unidade de medida não leva o “s” do plural nem o ponto final como abreviação (p. ex.: cm, m, kg etc.).
Os símbolos de medida aparecem depois do número, sem espaço entre eles (p. ex.: 4,2m; 3h).
Agora que você já viu todos os elementos que compõem uma tabela, que tal vermos um exemplo? Já estudamos que uma tabela tem como objetivo apresentar os dados agrupados, de maneira que uma pessoa interessada pode visualizar e compreender o que querem dizer aqueles dados. Você conhecerá, agora, os principais tipos de tabelas, que podem ser:
Uma tabela simples é aquela em que contém a variável que estamos estudando com sua respectiva contagem, ou seja, com sua frequência. A Tabela 1 apresenta uma tabela simples, com seus elementos básicos:
Tabela 1 - Casos de dengue nos bairros de uma cidade no mês de fevereiro de 2020
Fonte: a autora.
Como podemos observar, no exemplo da Tabela 1, há todos os elementos básicos apresentados.
Além disso, uma tabela simples pode ser temporal, geográfica ou específica (categórica). Uma tabela é considerada temporal quando as observações da variável ocorrem de acordo com tempo. A Tabela 2 traz um exemplo de série temporal ou histórica:
Tabela 2 - Casos de dengue no decorrer dos anos em uma cidade
Fonte: a autora.
Uma tabela simples, também, pode ser geográfica, quando a variável analisada é referente ao local ou território. Um exemplo de série geográfica pode ser observado na Tabela 3.
Tabela 3 - Alunos matriculados em um curso de Ciências Biológicas no estado do Paraná no ano de 2010
Fonte: a autora.
Uma tabela simples, também, pode ser específica ou categórica, quando a variável analisada é referente a categorias específicas. Um exemplo de série geográfica pode ser analisado na Tabela 4.
Tabela 4 - Número de alunos de uma instituição de ensino superior (EAD) no ano de 2015
Fonte: a autora.
Uma tabela, também, pode ser de dupla entrada, isso significa que temos a necessidade de apresentar em uma única tabela, mais dados estudados em uma variável, para isso, é preciso fazer uma junção de duas ou mais séries (CRESPO, 2009).
Uma tabela, também, pode ser de dupla entrada
Ao fazer esta junção dos dados para serem apresentados em uma única tabela, teremos: duas ordens de classificação, uma vertical (na coluna) e uma horizontal (nas linhas). Para apresentar uma tabela de dupla entrada, temos a Tabela 5, que trata do número de matrículas da Educação Básica do ano de 2019, e os dados estão apresentados (dupla entrada) a seguir:
Tabela 5 - Número de Matrículas da Educação Básica, por Etapa de Ensino, segundo a Região Geográfica, a Unidade da Federação e o Município – 2019
Fonte: adaptada de Inep (2020, on-line).
Na Tabela 5, podemos observar que a região (coluna) é referente às regiões no Brasil, já as etapas de ensino: Educação Infantil, Ensino Fundamental, Ensino Médio, Ensino Profissional, Educação de Jovens e Adultos e Educação Especial são analisados, também, nas colunas e linhas. Temos, então, um exemplo de tabela com a dupla entrada, ou seja, mais que uma variável sendo estudada, na qual podemos analisar as regiões brasileiras (geográficas) e etapas de ensino (categorias). Lembre-se de que, em uma tabela de dupla entrada: cada uma das respostas combinadas fica agregada em uma única célula.
Agora que você já conhece as tabelas simples bem como os tipos de série e a dupla entrada, que tal aprendermos a construir uma tabela do zero? Mas, antes, precisamos relembrar alguns conceitos matemáticos fundamentais aqui na Bioestatística, pois os cálculos das frequências precisam de duas grandezas: razão e proporção. Definir razão pode se tornar uma tarefa inglória se formos atrás de todos os significados para este termo (ARANGO, 2011). Aqui, trataremos da parte que aplicaremos na disciplina de Bioestatística, vejamos alguns exemplos:
Supondo que um corpo tem seis metros de comprimento, e outro corpo três metros, ao dividirmos o comprimento de um pelo outro, teremos:
63=2
Ainda, podemos afirmar que, o corpo é duas vezes o tamanho do menor, ou, ainda, que tem a metade do comprimento do maior, e esta divisão chamamos de razão .
A razão 12pode ser representada como 1:2, o que significa que cada metro do corpo menor corresponde a 2 metros do corpo maior.
Outro exemplo: dos 1.200 pacientes que procuram a emergência hospitalar na última semana, 240 eram idosos. A razão de idosos que procuraram a emergência esta semana foi de:
240 1200 = 240 ( 240)1200 ( 240)=15
Isto é, a cada cinco pacientes, um deles era idoso.
Segundo Parenti (2017, p. 49):
“ Os conceitos de razão e proporção estão relacionados entre si. Assim, a razão entre o quociente (divisão) entre dois números e a proporção é a igualdade entre duas razões. As proporções são aplicadas em situações em que as informações devem ser comparadas e são calculadas pelo uso de ‘regra de três simples’.
Para entender melhor a proporção, vejamos o exemplo a seguir: para produzir 600 pães no refeitório de um hospital, são utilizados 100 kg de farinha. Sendo assim, quantos pães podem ser feitos com 25 kg de farinha?
600x =10025
100.x=600.25
100x=1500
x=1500100
x=150
Assim, podemos dizer que é possível produzir 150 pães com 25 kg de farinha.
Agora que já relembramos os conceitos matemáticos necessários para construir uma tabela de frequências, você aprenderá passo a passo como elaborar. Vamos lá?
Primeiramente, trabalharemos com a organização dos dados: você organiza dados numéricos criando disposições ordenadas ou distribuídas . Para preparar seus dados coletados com o intuito de organizá-los, inicialmente, decidiremos se precisaremos analisar suas variáveis numéricas com base em grupos que sejam criados pelos valores de uma segunda variável categórica. Esta decisão afetará o modo como você prepara os dados.
De acordo com Levine, Stephan e Szabat (2016), caso decida analisar suas variáveis numéricas em grupos que sejam definidos pelos valores de uma segunda variável categórica, você deve, então, decidir se utilizará um formato empilhado ou não empilhado. Em um formato empilhado, todos os valores de uma variável numérica aparecem em uma única coluna, enquanto uma segunda coluna, em separado, contém os valores categorizados que identificadas a qual subgrupo pertence cada um dos valores numéricos. Em um formato não empilhado, os valores de uma variável numérica são divididos por subgrupos e colocados em colunas separadas.
Vamos ao exemplo supondo que você pretende comparar os custos em restaurantes localizados na cidade com os custos em restaurantes localizados em bairros. Para preparar esses dados de forma não empilhada, poderia ser criada uma coluna para a variável custo com alimentação e outra coluna para a variável localização, uma variável categórica com os valores de cidade e bairros. Observe o custo de 20 refeições, no Quadro 2 a seguir:
Quadro 2 - Disposição de dados não empilhados
Fonte: a autora.
Você pode observar que, desta forma, fica um pouco mais complexo trabalharmos com os dados. Este modelo de não empilhados foi apresentado para que você tenha ciência de como trabalhar com os dados. Mas se observarmos esses dados, fica difícil tomarmos conclusões acerca dos custos das refeições, como qual valor (em R$) que mais aparece (mais se repete), certo? Nem qual percentual deste valor pago dentre estas 20 refeições. Podemos facilitar a análise dos nossos dados quando trabalhamos com a disposição de dados ordenados , ou seja, quando colocamos os dados em rol.
Segundo Levine, Stephan e Szabat (2016), uma disposição ordenada organiza os valores de uma variável em ordem de classificação, partindo do menor valor para o maior, ou seja, organizamos os dados em uma lista (crescente). Uma disposição ordenada pode ajudar a obter mais entendimento entre a amplitude dos valores em seus dados e é, particularmente, útil quando você tem mais do que um valor se repetindo. Veja, no Quadro 3, os mesmos dados apresentados anteriormente, de maneira ordenada.
Quadro 3 - Disposição de dados não empilhados em rol
Fonte: a autora.
Análise, no Quadro 3, que fica bem mais fácil trabalhar com os dados seguindo uma ordem crescente, ou seja, do menor valor para o maior valor . Outro exemplo clássico de rol que, certamente, você já viu em sala de aula, é a lista de presença dos seus alunos. Os nomes estão em ordem alfabética, ou seja, em um rol, assim, fica mais fácil para localizar algum aluno, porque os dados estão organizados. Além disso, o rol é um passo importante para construção de tabelas de frequências. Mas o que são tabelas de frequências? Trata-se de uma distribuição, de modo tabular, dos valores de uma variável numérica em um conjunto de classes (linhas) numericamente ordenadas . Podemos ter uma distribuição de frequências com intervalo de classes e sem intervalo de classes.
Primeiro, você aprenderá a construir uma distribuição de frequências sem intervalo de classes, utilizando a contagem de uma variável qualitativa nominal. Vejamos a situação a seguir: um professor do curso de Enfermagem, aplicou um questionário para entender, qual(is) disciplina(s) os alunos tinham como preferência em uma turma. Para isso, selecionou uma turma com 40 alunos e fez a seguinte pergunta: “Qual disciplina você mais gosta neste ano?” Dentre as opções dadas aos alunos eles tiveram:
Dentre as opções dadas aos alunos eles tiveram:
Os votos dos 40 alunos podem ser verificados a seguir (Quadro 4).
Quadro 4 - Votos dos 40 alunos de uma turma sobre a preferência de disciplinas (brutos)
Fonte: a autora.
Para facilitar a construção da nossa tabela, faremos um rol, utilizando as disciplinas com ordem alfabética (Quadro 5).
Quadro 5 - Votos dos 40 alunos de uma turma sobre a preferência de disciplinas (em rol)
Fonte: a autora.
Agora que temos os dados em rol, construiremos a tabela de frequências (Fi), que se trata de agrupar os dados em uma tabela, contando quantas vezes cada variável (nesse caso, cada disciplina) se repetiu, isso é o que chamamos de frequência. Para isso, organizamos a tabela (utilizando a ordem alfabética), contendo todos os elementos (título, cabeçalho, linhas, entre outros). Utilizando os dados em rol, construiremos uma tabela de frequências com a preferência de 40 alunos de uma turma do curso de Enfermagem (Tabela 6).
Tabela 6 - Distribuição de frequências referentes à preferência de 40 alunos de uma turma do curso de Enfermagem
Fonte: a autora.
Como você pode observar, inserimos a coluna contagem somente para você entender como funciona a distribuição de frequência, geralmente, ela não aparece, mas como é a primeira vez que você está construindo essa tabela, elaboramos essa coluna para melhor entendimento. Observe que, na disciplina Anatomia Humana , a repetição, ou seja, a contagem foi de sete alunos, portanto, a frequência desta classe (desta linha) é igual a sete. Já na segunda classe, ou seja, segunda linha, temos a disciplina Bioestatística , com votos de seis alunos, portanto, a frequência para esta disciplina é igual a seis.
Enquanto na terceira classe, a contagem para disciplina de Biologia Celular e Molecular é igual a nove, sendo assim, na coluna frequência, inserimos a informação que é igual a nove. Por fim, na última classe, com a disciplina Parasitologia , teve a preferência de 18 alunos. Uma classe em uma distribuição de frequência corresponde ao número de linhas desta tabela, exceto cabeçalho e total. Podemos, entretanto, reconstruir esta tabela, inserindo algumas colunas complementares que são importantes em uma distribuição de frequência, tais como:
corresponde à proporção entre a frequência da classe pelo total de números observados, e a equação a seguir apresenta-nos como calcular a frequência relativa. Fr(%)=Fin.100
Em que: Fr (%) = Frequência relativa (em percentual) Fi = Frequência da classe n = número total de elementos (ou somatória das frequências, correspondente ao total).
trata-se de uma classe em que a frequência acu- mulada da classe, dividindo
pelo total da distribuição, ou seja, pelo total. A equação referente à
frequência acumulada pode ser observada a seguir:
Frac(%)=Facn.100
Em que:
Frac (%) = Frequência relativa acumulada (em percentual)
Fi = Frequência acumulada da classe
n = número total de elementos (ou somatória das frequências, correspondente
ao total).
Agora, você aprenderá a construir a tabela de distribuição de frequências com estas colunas complementares (Tabela 7). Vamos lá!
Tabela 7 - Distribuição de frequências referentes a preferência de 40 alunos de uma turma do curso de Enfermagem
Fonte: a autora.
Como você pode observar, apresentamos as colunas FR (%), Fac e FRAC (%) com todas as fórmulas e resoluções.
Na coluna FR (%), utilizamos a equação a seguir:
Frac(%) = Facn.100
Em seguida, substituímos cada valor da frequência, dividimos pelo total (que neste caso é igual a 40), e temos que a proporção de alunos que preferem a disciplina Anatomia Humana é de 17,5%. Essa coluna também serve para situações em que queremos saber a proporção em percentual, por exemplo: qual o percentual de alunos que preferem a disciplina de Biologia Celular e Molecular? Simplesmente, basta olhar na coluna FR (%) e responder que: 22,5% dos alunos preferem a disciplina Biologia Celular e Molecular .
Neste momento, você pode estar se questionando, quando construirá tabelas de frequências e se é preciso apresentar todos os cálculos nesta tabela. A resposta é: não, necessariamente. No exemplo apresentado, fizemos a resolução completa apresentando os cálculos em cada uma das classes para que você possa visualizar a equação correspondente bem como a substituição dos valores para compor a tabela.
Como você pode perceber, não precisamos apresentar todos os cálculos nas colunas complementares da tabela de distribuição de frequências. Estudante, convido-o(a), agora, a assistir ao vídeo sobre o passo a passo da construção das colunas complementares bem como reescreverei essa tabela sem cálculos. Ouça o podcast no seu ambiente virtual de aprendizagem.
Na maioria das vezes, quando elaboramos estas tabelas, normalmente, não apresentamos os cálculos. Agora, você verá a mesma tabela, sem apresentar os cálculos (Tabela 8).
Tabela 8 - Distribuição de frequências referentes a preferência de 40 alunos de uma turma do curso de Enfermagem (sem os cálculos)
Fonte: a autora.
Além disso, temos como ir tirando prova real para verificar se os cálculos apresentados estão corretos. Observe a seguir:
observe que a somatória das frequências deve ser igual ao número de elementos coletados, ou seja, para este caso, foram entrevistados 40 alunos do curso de Enfermagem, então, a somatória deve ser igual a 40.
analise que a somatória das frequências relativas em percentual, a somatória deve ser igual a 100, correspondente a 100 por cento. Caso sua somatória dê, por exemplo, 98%, é necessário conferir os cálculos anteriores.
aqui, somamos as frequências das classes com as frequências posteriores, certo? Mas a prova real, trata-se do último valor encontrado na coluna FAC ser igual ao total de elementos analisados, ou seja, o valor dever ser igual ao total da somatória da coluna frequência. Na coluna Frequência Relativa Acumulada (FRAC %)
o último valor correspondente à variável analisada deve ser igual a 100.
Em uma tabela de distribuição de frequências, você sabia que podemos tirar a prova real dos cálculos nas colunas complementares? Sim, isso é possível e, para entender como fazer essa prova real, convido você a acessar este vídeo e fazer comigo o passo a passo. Você verá que não terá erro. Assista ao vídeo no seu ambiente virtual de aprendizagem.
Não se esqueça: o coração da sua tabela é a coluna frequência, por isso, é importante estes valores serem distribuídos de maneira correta.
Figura 1 - Passo a passo para construção de uma tabela de frequências simples, sem intervalo de classes
Fonte: a autora.
Até agora, vimos como trabalhar com uma distribuição de frequências, sem intervalo de classes, mas com uma variável quantitativa discreta. Vejamos um exemplo: supondo que um diretor de uma escola anotou durante 30 dias o número de atendimento aos pais e obteve o seguinte resultado:
Colocaremos os dados em rol.
.png)
Construir a tabela, distribuir as frequências.
.png)
Construir as colunas complementares (já realizado na própria tabela). Agora é só conferir mais uma vez a tabela e verificar se está tudo de acordo.
As tabelas têm a função de condensar informações, em alguns casos, o número de dados é tão grande, que dificulta a análise, para estes casos, são utilizadas tabelas com dados agrupados em intervalos de classes.
Tabela 9 - Distribuição de frequências referentes ao atendimento do diretor de uma escola durante 30 dias consecutivos
Fonte: a autora.
Imagine a seguinte a situação: você já atuando como professor de cursos de Saúde, aplica uma prova a seus alunos. Para entender o desempenho dos seus alunos nesta avaliação, você pode fazer uma lista com as notas dos seus alunose colocá-las ordenadas. A seguir temos as notas dos alunos desta turma (dados brutos).
Tabela 10 - Distribuição de frequências referente às notas de seus alunos (sem intervalo de classes)
Fonte: o autor.
Você pode observar que temos uma tabela com mais de dez classes, ou seja, mais do que dez linhas (exceto cabeçalho e total). Agora, imagina, quando formos inserir as colunas complementares, quantos números terá nossa tabela?
Para melhorar essa tabela, podemos construir uma distribuição de frequências com intervalo de classes para condensar melhor as informações da tabela. Ao elaborar uma distribuição de frequências com intervalo de classes, precisamos seguir os passos:
colocar os dados em rol.
determinar a amplitude total, que se trata da diferença entre o maior valor
do conjunto de dados pelo menor valor do conjunto de dados, resolvido pela
equação:
AT=Xmáx - Xmín
Em que: AT = Amplitude Total Xmáx = Maior valor do conjunto de dados Xmín =
menor valor do conjunto de dados
determinar o número de classes. Para uma distribuição de frequências com
intervalo de classes, os números de linhas são definidos pela equação a
seguir:
k=n
Em que: K = número de classes n = número total de elementos Obs.: é muito
importante que o número de classes seja arredondado.
determinar a amplitude do intervalo, ou seja, a distância entre o limite
inferior da classe e o limite superior da classe, dado pela equação:
h=ATk
Em que:
h = Amplitude do intervalo
AT = Amplitude total
k = número de classes
construa a tabela, faça as colunas complementares, distribuindo, corretamente, as frequências.
O arredondamento de dados é importante em uma distribuição de frequências com intervalo de classes, principalmente no item número de classes. Para relembrar como se faz o arredondamento de dados, assista ao vídeo a seguir.
A seguir, temos um resumo dos passos que devem ser seguidos para construir uma distribuição de frequências com intervalo de classes (Figura 2).
Figura 2 - Passo a passo para construção de uma tabela de frequências com intervalo de classes
Fonte: o autor.
Para entender melhor a construção de uma distribuição de frequências com intervalo de classes, observe os dados a seguir, que são referentes às notas de alunos do curso de Ciências Biológicas:
colocar os dados em rol ordenado (crescente).
agora, determinaremos a Amplitude do Intervalo:
AT=Xmáx-Xmín
AT = 10,0-3,0=7,0
Antes de construir nossa tabela de frequências, precisamos entender o que são limites inferiores e superiores. Temos quatro maneiras de utilizar os limites inferiores e superiores:
incluímos o limite inferior e excluímos o limite superior.
Nesta notação, excluímos o limite inferior e incluímos o limite superior.
Nesta notação, excluímos ambos os limites.
Nesta notação, incluímos ambos os limites.
Qual delas usar? Utilizaremos a primeira notação, que inclui limite inferior e exclui limite superior, mas, em alguns casos, somente na última classe, teremos que usar a quarta notação, que inclui ambos os limites, isso pode ocorrer para que o maior valor do conjunto de dados seja contado.
Como já temos todas as informações, construiremos nossa tabela (Tabela 11):
Tabela 11 - Distribuição de frequências referente às notas de seus alunos (com intervalo de classes)
Fonte: o autor.
Agora, temos a tabela resolvida, observe que, na última classe, tivemos que utilizar a notação que inclui limite inferior e inclui limite superior |-----|, isso foi feito para que a nota 10,0 fosse incluída na contagem.
Observe, nesta tabela, que há uma coluna complementar a mais, a coluna ponto médio, que é determinado pela equação:
Xi= (Li+Ls)2
Em que:
Ponto médio
Limite inferir do intervalo de classe (independentemente da notação)
Limite superior do intervalo de classe (independentemente da notação)
É importante ficar atento porque só existe um ponto médio em uma distribuição de frequências com intervalo de classes.
Outra maneira de apresentar os dados provenientes de uma pesquisa são os gráficos (Figura 3). Um gráfico tem por objetivo apresentar uma ideia visual do comportamento de um conjunto de valores , tem a vantagem de facilitar a compreensão de determinada situação que queira ser descrita, permitindo a interpretação rápida de suas principais características (ARANGO, 2011).
Você sabia que um professor pode trabalhar dados da Educação Básica e do Ensino Superior, fazendo consulta no próprio INEP? E que estes dados podem ser utilizados para entender o comportamento dos alunos do país? E que você pode trabalhar isso em sala de aula utilizando esses dados? Nossa roda de conversa traz uma explicação do trabalho de coleta dos dados do INEP e da organização em tabelas, planilhas e gráficos. O vídeo estará disponível no seu ambiente virtual de aprendizagem.
É importante frisar que um gráfico não traz tantas informações quanto a uma tabela. E você vai se perguntar: usarei gráficos ou tabelas em minhas pesquisas? A resposta é: fica a critério do pesquisador, ou seja, a pessoa que está fazendo a pesquisa pode utilizar gráficos ou tabelas, ou fazer uma mesclagem entre eles. Os gráficos estão sempre presentes em trabalhos científicos, artigos, congressos, seminários, simpósios, em que é preciso comunicar um grande volume de informações com tempo limitado, de forma compreensível e agradável.
Temos vários modelos de gráficos, que veremos a seguir:
Gráfico de colunas
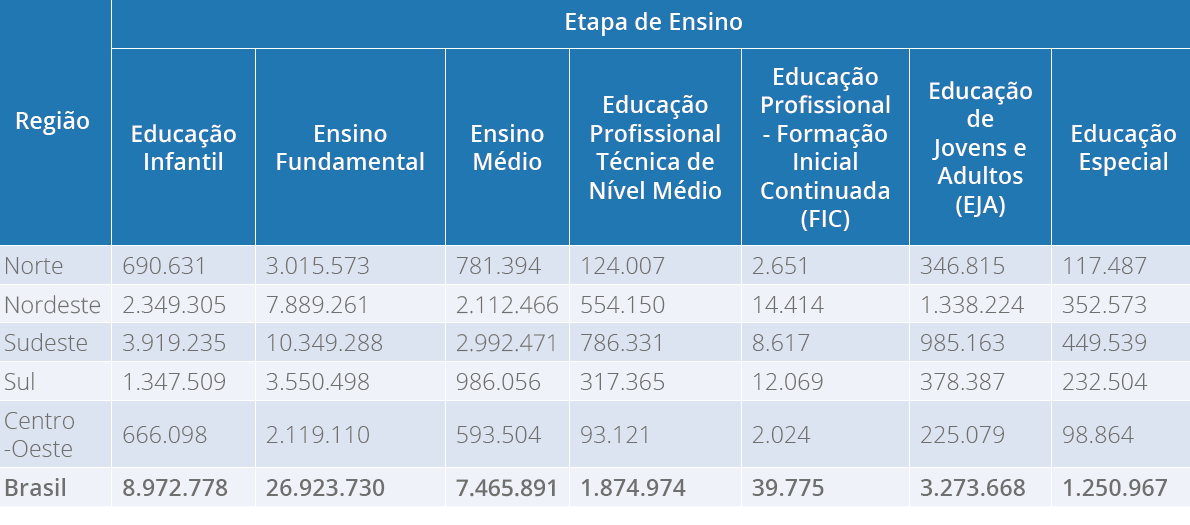
quando temos as categorias apresentadas no eixo horizontal e a frequência no eixo vertical (BARBETTA, 2014). Para construção do gráfico de colunas, utilizaremos os dados referentes às matrículas na Educação Infantil, retirados do INEP (2019). A Figura 3, apresenta um gráfico de colunas:
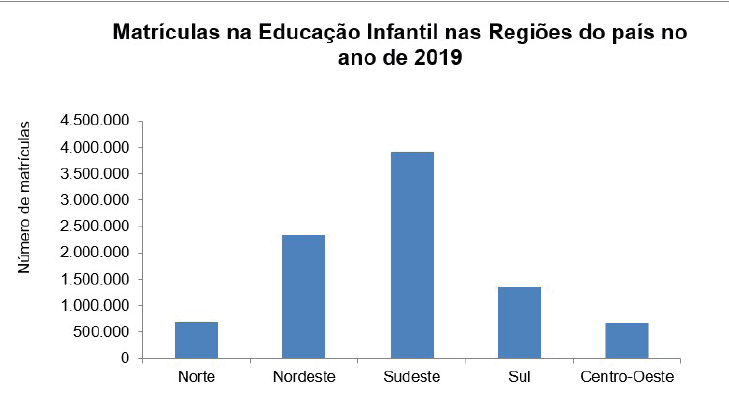
Figura 3 - Gráfico de Colunas
Fonte: adaptada de Inep (2020).
Como você pode observar, na horizontal, temos as regiões do país e, na vertical, temos o número de matrículas na Educação Básica. Caso você queira saber o número de matriculados na região Norte, por exemplo, basta olhar na região Norte e verificar que há pouco mais do que 500.000 matrículas, no ano de 2019.
Gráfico de barras
em que cada variável é representada por uma barra de comprimento proporcional à sua ocorrência (BARBETTA, 2014). Temos as barras na vertical, na Figura 4.
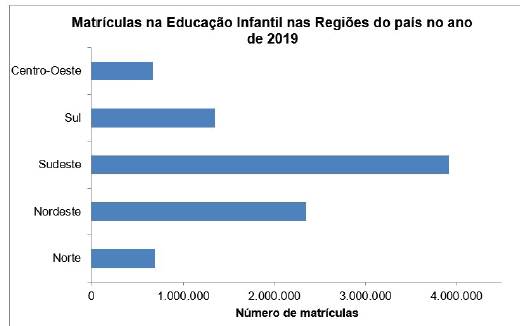
Figura 4 - Gráfico de Barras
Fonte: adaptada de Inep (2020).
Gráfico de linhas
são gráficos bem interessantes no uso de séries temporais, ou seja, a variável predominante é o fator tempo (cronológico), esse tipo de gráfico mostra informações da série estudada em pontos e que são marcados por segmentos de linha reta. A Figura 5 apresenta-nos um gráfico de linhas.
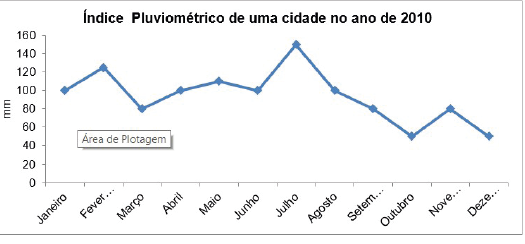
Figura 5 - Gráfico de linhas
Fonte: a autora.
Gráfico de setores
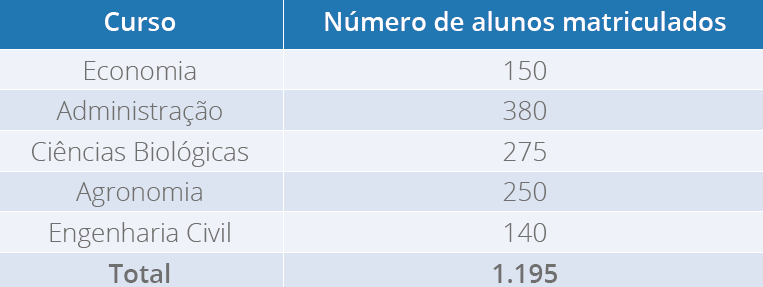
também conhecido como gráfico de pizza, é um gráfico circular, em que os valores são representados proporcionais às respectivas frequências. Para a construção deste gráfico, utilizaremos os dados referentes às preferências de alunos de uma turma do curso de Ciências Biológicas (Figura 6).
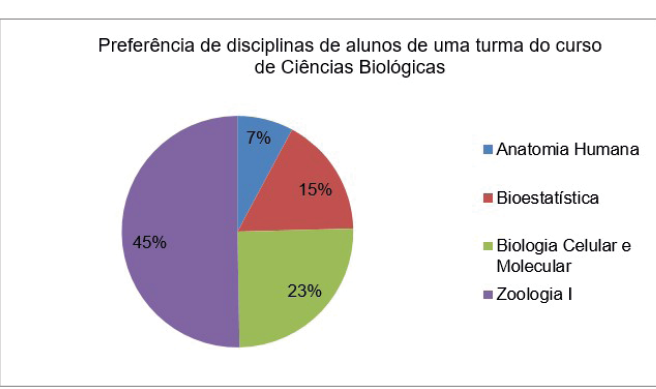
Figura 6 - Gráfico de setores
Fonte: a autora.
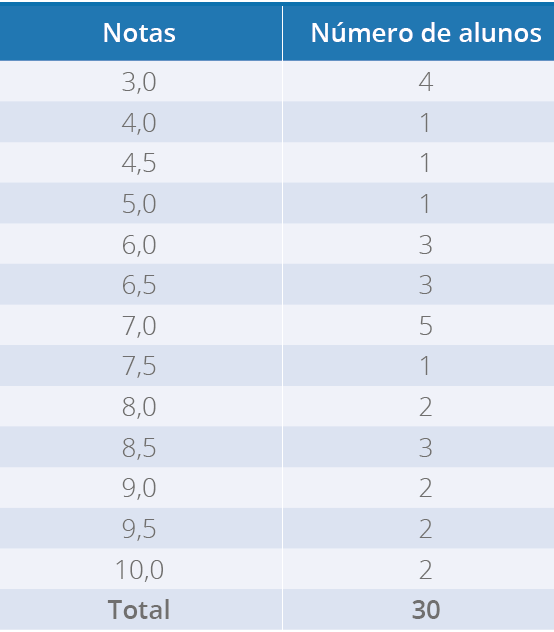
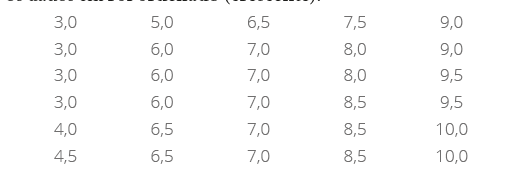
Histograma
é a representação gráfica de uma distribuição de frequências, pode ser construído a partir de uma distribuição de frequências sem intervalo de classes ou com intervalo de classes. Aqui cada retângulo justaposto representa uma classe (Figura 7).
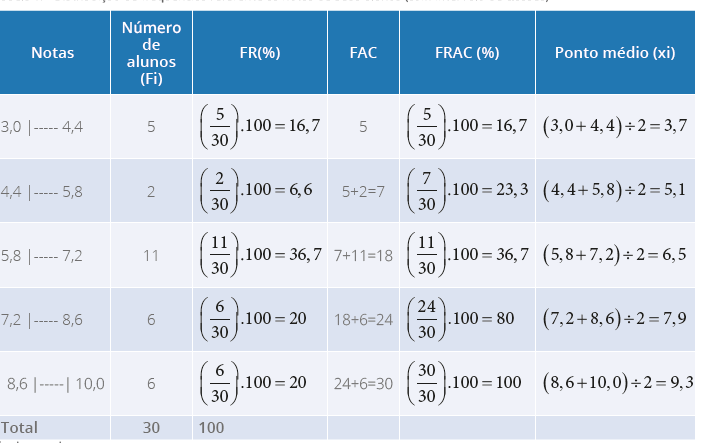
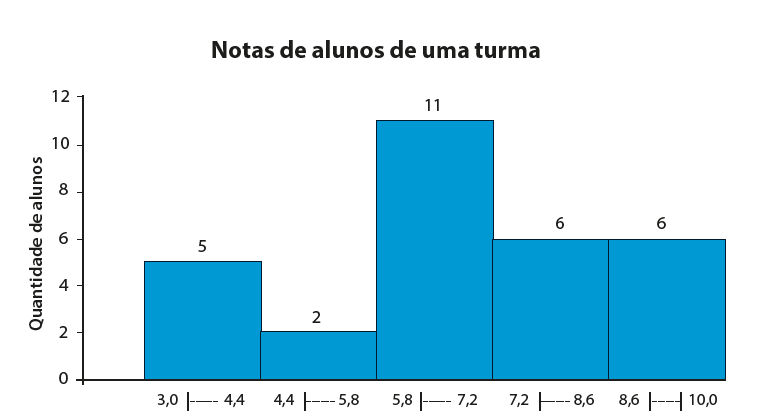
Figura 7 - Histograma
Fonte: a autora.
Na Figura 7, que representa um histograma, para interpretação, você deve olhar as notas bem como a quantidade de alunos, observe que, no primeiro retângulo, temos cinco alunos com notas maiores ou iguais a 3,0 e menores do que 4,4, e assim sucessivamente.
Você pode, também, construir todos os seus gráficos em suas pesquisas com o auxílio do Microsoft Excel®, basta inserir todos os dados, selecionar e escolher o modelo que melhor represente os dados com que está trabalhando. Dessa maneira, fica a critério do pesquisador a utilização de tabelas e gráficos para apresentar os resultados de uma pesquisa, podendo seu uso ser intercalado.
Você percebeu o quanto a construção de tabelas e gráficos pode ser significativa e aplicada na sua profissão? Existem muitas possibilidades. Você pode trabalhar com pesquisa e apresentar os resultados em tabelas e gráficos, com dados disponíveis no próprio INEP sobre a Educação Básica ou, até mesmo, coletar dados de seus alunos, construir tabelas e gráficos para entender o comportamento de sua turma em alguns quesitos (dê preferência por disciplinas, notas, frequências, evasões, entre outros) Veja que tudo isso está relacionado e que a Bioestatística está presente em sua na vida diária.
Você sabia que, como futuro da saúde e, possivelmente, um profissional da Educação, faz parte do exercício de cidadania e profissional a consulta de dados básicos para articulação, conscientização e tomada de decisão? Para tanto, uma sugestão seria iniciarmos consultando a sinopse Estatística da Educação Básica. Esta sinopse trata-se de dados relacionados à matrícula de acadêmicos, ao estabelecimento, às regiões, ao rendimento escolar para as diferentes modalidades de ensino brasileiras: Ensino Regular (Educação Infantil e Ensino Fundamental e Médio), Educação Especial e Educação de Jovens e Adultos. Você pode consultar os dados dessa sinopse que serão apresentados, detalhadamente, por cidade, estado e região, e trabalhar com eles os apresentando em tabelas mais reduzidas. Tudo isso pode variar de acordo com a sua necessidade como futuro professor. Clique aqui.
Estudante, vimos em nossos estudos, como as técnicas de estatística são fundamentais para tomada de decisões e que, para organizar uma tabela, precisamos seguir algumas normas específicas que foram apresentadas no decorrer desse conteúdo. Além disso, os gráficos também podem ser utilizados para visualizar o resultado de uma pesquisa.
Assim, ao tabular os resultados da pesquisa propostos no início de nosso estudo, mais especificamente na experimentação, em que colocamos uma situação hipotética, que realizará um experimento para saber se as pessoas de um bairro (ou membros da família tiveram dengue). Aqui, na ação, após toda coleta de dados a partir de um formulário elaborado por você, certamente, terá resultados a serem tabulados.
É isso mesmo, com todas as técnicas estudadas, você poderá criar tabelas de frequências, colunas complementares para melhorar os resultados obtidos e, a partir de então, tomar decisões. Supondo que suas respostas sejam que, dentro de um grupo de dez pessoas, oito responderam que já tiveram dengue, ou seja, 80% dos entrevistados, como profissional da área de Ciências Biológicas e Saúde, o que você pode propor?
Com base nesse estudo, pôde propor palestras para sensibilização da população, um dia D de combate ao foco de dengue, orientar, disseminar informações acerca dos cuidados que devemos ter com a dengue. Aqui, você pode perceber, que usamos uma técnica estatística, e a partir de então, foram feitas ações de melhoria no combate à dengue.
Espero que tenha tirado o máximo proveito desse conteúdo.
ABNT. NBR 14724:2011 - Informação e documentação - Trabalhos acadêmicos – Apresentação. Rio de Janeiro: ABNT, 2011.
ARANGO, H. G. Bioestatística: teórica e computacional: com banco de dados reais em disco. 3. ed. Reimpr. Rio de Janeiro: Guanabara Koogan, 2011.
BARBETTA, P. A. Estatística aplicada às Ciências Sociais. 9. ed. Florianópolis: UFSC, 2014.
CRESPO, A. A. Estatística. 19. ed. São Paulo: Atlas, 2009.
IBGE. Normas de apresentação tabular. 3. ed. Rio de Janeiro: IBGE, 1993.
INEP. Sinopse Estatística da Educação Básica 2019. Brasília: Inep, 2020. Disponível em: http://portal. inep.gov.br/sinopses-estatisticas-da-educacao-basica. Acesso em: 17 maio. 2021.
LEVINE, D. M.; STEPHAN, D. F.; SZABAT, K A. Estatística – Teoria e Aplicações. Usando Microsoft Excel em Português. 7. ed. Rio de Janeiro: LTC, 2016.
PARENTI, T. M. S.; SILVA, J. S. F. da.; SILVEIRA, J. Bioestatística. Porto Alegre: SAGAH, 2017.
