TEMA DE APRENDIZAGEM

Medidas De Frequência E De Associação

MINHAS METAS

Olá estudante,

Seja bem-vindo(a) ao tema Medidas De Frequência E De Associação! Neste conteúdo você irá conhecer e introduzir os conceitos e aplicações de prevalência e incidência, e abordar a relação prevalência e incidência, descrever os tipos de prevalência e sua interpretação, os tipos de incidência e sua interpretação. E por fim, conceituar e interpretar as medidas de associação utilizadas para identificação de fatores de risco ou de proteção dos estudos retrospectivos, além das medidas de associação utilizadas para identificação de fatores de risco ou de proteção dos estudos prospectivos. Vamos lá?

Ao final deste tema de aprendizagem você será capaz de:

Conhecer e introduzir os conceitos e aplicações de prevalência e incidência.
Abordar a relação prevalência e incidência, descrever os tipos de prevalência e sua interpretação, os tipos de incidência e sua interpretação.
Conceituar e interpretar as medidas de associação utilizadas para identificação de fatores de risco ou de proteção dos estudos retrospectivos.

Inicie sua jornada

Estudante aqui você aprenderá o que são e como utilizar as medidas de ocorrência dos fenômenos epidemiológicos , como a prevalência e a incidência. Nós também abordaremoscomo calcular e interpretar as medidas de associação ( Odds ratio , ou razão das proporções, e risco relativo), as quais possibilitam identificar fatores de risco associados aos desfechos em saúde e calcular a probabilidade da ocorrência dos problemas de saúde quando um indivíduo é exposto a esses fatores.

Faremos uma breve introdução dos conceitos básicos das medidas de ocorrência mais utilizadas em epidemiologia, também chamadas de medidas de frequência. Também mostraremos para você como representar a ocorrência das doenças nas populações utilizando tabelas, mapas e gráficos. Descreveremos as medidas de prevalência e de incidência, seus cálculos e interpretações. Nesses dois tópicos, utilizaremos exemplos hipotéticos ou originais para que você compreenda a aplicação dessas medidas, para verificar a situação de saúde das populações e determinar quais são as doenças ou causas das enfermidades que nelas ocorrem com maior frequência.

E conceituaremos as medidas de associação e suas aplicações para a identificação de fatores de risco, causas ou ainda fatores de proteção, que levam à ocorrência de doenças, óbitos ou outros desfechos em saúde. Para facilitar a compreensão das medidas de associação, destacaremos as medidas de odds ratio (proporção dos pares) e risco relativo, utilizadas quando se realizam estudos retrospectivos e prospectivos, respectivamente.

Desenvolva seu potencial

MEDIDAS DE FREQUÊNCIA (OCORRÊNCIA)

Figura 1 – Gráfico de ocorrência do vírus HIV.

Fonte: Wikimedia (2014, on-line)¹.

Nesta unidade, conceituaremos as medidas de frequência, também chamadas de ocorrência, e as medidas de associação. Você será capaz de compreender e até de calcular e interpretar as medidas de frequência e de associação a partir da obtenção dos conhecimentos teóricos. Primeiramente vamos conceituar as medidas de frequência das doenças.

Para isso, precisamos voltar ao conceito de epidemiologia contido anteriormente, na qual o melhor conceito da disciplina foi descrito por Almeida Filho e Barreto (2011, on-line):

“ ciência que estuda o processo saúde-enfermidade na sociedade, analisando a distribuição populacional e fatores determinantes do risco de doenças, agravos e eventos associados à saúde, propondo medidas específicas de prevenção, controle ou erradicação de enfermidades, danos ou problemas de saúde e de proteção; promoção ou recuperação da saúde individual ou coletiva, produzindo informação e conhecimento para apoiar a tomada de decisão no planejamento, administração e avaliação de sistemas, programas, serviços e ações de saúde. Podemos ver que o objetivo da Epidemiologia é verificar a distribuição dos determinantes das doenças, dos agravos e de outros eventos ligados à saúde nas populações.

VOCÊ SABE RESPONDER?

Contudo, qual é a ferramenta dos epidemiologistas para verificar e analisar essa distribuição? Destacamos aqui a importância e a utilização das medidas de frequência das doenças e outros desfechos nas populações. Para explorar melhor a ocorrência das doenças e sabendo-se que os riscos das doenças são afetados pelos fatores pessoais, de tempo e lugar, precisamos perguntar (GORDIS, 2009): Quem foi acometido pela doença? Quando a doença ocorreu? De onde surgiram os casos?

As medidas de frequência/ocorrência são aquelas que medem a ocorrência (número, porcentagem, taxa ou proporção) de um evento (óbito, doença, nascimento e etc.) em uma população ou em grupos específicos, em determinado período e local (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011).

Pensando Juntos

Em relação às populações, é evidente que as características do hospedeiro humano, como a raça, a idade e o sexo, influenciam a ocorrência das doenças (GORDIS, 2009). O tempo Quando nos indicará a periodicidade com que as doenças ocorrem; se é contínua (veja a figura a seguir), sazonal (de acordo com a estação climática) ou cíclica (ocorre sempre de tempos em tempos), permitindo a identificar a tendência desta ocorrência, ou seja, se ocorre diminuição, manutenção ou aumento do número de casos. Tomemos como exemplo o gráfico em linha na figura a seguir (BRASIL, 2017):

Percentual de casos de violência - Por sexo

Figura 2 - Frequência (%) de casos de violência de acordo com o sexo, de 2009 a 2016, no Brasil.

Fonte: Ministério da Saúde ([2018], on-line)².

Neste gráfico, disponibilizado pelo Ministério da Saúde, verificamos que o maior número de casos de violência ocorre no sexo feminino e que, de acordo com os anos, o número de casos mantém uma constância e é quase duas vezes maior nas mulheres que nos homens. No exemplo acima, foi utilizada representação gráfica do tipo linear para mostrar a frequência dos casos de violência. Veja que a discussão do porquê o maior número de casos ocorre nas mulheres ainda não é feita.

Essa análise qualitativa não será trabalhada aqui, até porque são necessários muitos outros dados e informações. A pergunta Onde indicará a distribuição geográfica da doença; pode ser em um bairro, uma cidade, uma zona rural, um estado, um país ou ser global. Destacamos aqui a variável lugar (UNAIDS, 2008):

Figura 3. Prevalência global de HIV/AIDS em adultos jovens (15 a 49 anos) no ano de 2008. / Fonte: Wikimedia (2015, on-line)³. Representação gráfica da distribuição geográfica da infecção pelo HIV/AIDS no mundo. As áreas mais vermelhas são aquelas de maior ocorrência de infecção pelo HIV/AIDS, e as áreas em cinza não há dados de distribuição da infecção.

VOCÊ SABE RESPONDER?

Você conhece as doenças mais frequentes em seu município, estado e país? No Brasil, as doenças mais frequentes e que mais matam são as doenças cardiovasculares e as neoplasias.

Aprofundando

As fontes de dados utilizadas para se obter as informações de uma pessoa doente, o período e o local da doença são provenientes de registros contínuos, como as Declarações de óbito, notificações (sistemas de informação), prontuários médicos e hospitalares, ou ainda registros periódicos como os inquéritos epidemiológicos e estudos científicos (GORDIS, 2009; PEREIRA, 2003).

Os dados podem ser representados utilizando cartogramas (distribuição dos casos de acordo com a área geográfica, por exemplo, a figura 2) e diagramas (linear ou tabular, veja a figura 1). A partir dos cartogramas, podemos compreender a distribuição da doença conforme o lugar (alas de um hospital, bairros, municípios, países, ou global), e os diagramas podem trabalhar diversas variáveis como, a frequência da doença de acordo com tempo, lugar e pessoa. O diagrama pode ser linear, como na figura 1, utilizando linhas ou ainda barras (como na figura 3). outra forma de representar os dados é utilizando tabelas (FRANCO; PASSOS, 2011).

Mas como medir os fenômenos?A ocorrência das doenças pode ser medida utilizando-se taxas ou proporções. As taxas mostram a rapidez de ocorrência de uma doença numa população, e as proporções nos mostram a fração da população que é afetada por aquele fenômeno. As medidas de ocorrência de uma doença é também chamada de medida de morbidade, em que estão incluídas a prevalência e incidência; também existem as medidas de mortalidade (GORDIS, 2009; FRANCO; PASSOS, 2011).

Resumidamente, a medida de prevalência é aquela utilizada para verificar a frequência de casos novos e antigos de uma doença, enquanto que a incidência refere-se apenas aos casos novos de uma enfermidade. A seguir, definiremos os conceitos, cálculos e interpretações das medidas de frequência de prevalência e incidência.

PREVALÊNCIA

A prevalência é definida como o número de pessoas afetadas por um fenômeno (doença ou agravo) na população em um determinado momento , dividido pelo número de pessoas na população no mesmo momento. Podemos dizer que a prevalência é a proporção de pessoas doentes naquele período estudado. O cálculo de prevalência se dá pela seguinte fórmula (GORDIS, 2009; FRANCO; PASSOS, 2011.

Taxa de prevalência a cada 1.000 pessoas é igual ao número de casos existentes de uma doença.

Taxa de prevalência a cada 1.000 pessoas= n° de casos existentes (novos e antigos) de uma doença ou outro fenômeno em um período de tempo, dividido pelo número de pessoas da população naquele mesmo período. Esse resultado deve ser multiplicado por 1.000.

O coeficiente de prevalência pode ser pontual (com tempo determinado) ou calculado para um período de estudo (GORDIS, 2009). Por exemplo: podemos calcular a prevalência de diabetes mellitus entre os anos de 2000 a 2010. Portanto, temos o número de casos existentes, num período e área, dividido pela população naquele mesmo período e lugar. O resultado pode ser multiplicado por 100, tendo o resultado calculado como uma porcentagem, por exemplo:

Em um município X (hipotético), durante os anos de 2008 a 2010, existiam 200 casos de diabetes mellitus , e a população total era de 2.000 habitantes. Temos 200 casos existentes divididos por 2.000, resultando em 0,1 que, multiplicado por 100 (%), mostra uma prevalência de 10% de diabetes mellitus na população do município X.

Podemos também calcular a prevalência multiplicando o resultado da fórmula por 1.000, 10.000, 100.000, um milhão, etc. A escolha do 10n é arbitrária (GORDIS, 2009), e pode ser escolhida para fazer comparações com outros coeficientes já obtidos, ou com o de outros lugares. Recomendamos que se tenha bom senso na escolha da potência, ou seja, para um lugar em que se tem apenas 10.000 pessoas, o uso do milhão como fator de multiplicação dará um número muito alto e de difícil compreensão pelos leigos . Veja o exemplo abaixo:

Dados hipotéticos: 200 casos existentes de hipertensão arterial/10.000 pessoas= 0,02 multiplicado por um milhão = 20.000, esta é a prevalência a cada um milhão de pessoas, mas esse lugar estaria muito longe de ter um milhão de pessoas. Ficaria mais expressivo e compreensível fazer o cálculo a cada 10.000 ou 1.000 pessoas, veja:

0,02 x 10.000= a prevalência é de 200 casos a cada 10.000 pessoas naquele período ou tempo;

0,02 x 1.000= a prevalência é de 20 casos a cada mil pessoas naquele momento ou período.

Dizemos que a prevalência é uma medida de frequência retrospectiva, uma vez que conta com o número de casos antigos e do presente, refletindo o passado até o momento da pesquisa (GORDIS, 2009). Um exemplo de retrospectivo: realiza-se um estudo no ano de 2017 e utilizam-se dados dos anos de 2000 a 2015 para verificar a prevalência de uma doença, ou seja, a pesquisa utiliza dados do passado e do momento da pesquisa. Na prevalência, não levamos em consideração a duração da doença (GORDIS, 2009), isto é, podemos ter pessoas com 10 a 20 anos de duração de uma doença, como a artrite reumatoide. Consequentemente, essas pessoas sempre farão parte do numerador (GORDIS, 2009).

Portanto, a prevalência pode ser considerada uma fotografia da doença naquele lugar e tempo, sendo uma medida estática. É também muito útil para medir a frequência e a magnitude de problemas crônicos, como a diabetes mellitus , a hipertensão arterial, as neoplasias e outras doenças de longa duração ou com longo período de latência, como a infecção pelo HIV e as hepatites virais (GORDIS, 2009; FRANCO; PASSOS, 2011). Na figura 4, temos a representação gráfica na forma de barra da distribuição da prevalência da infecção pelo HIV e morte, nos EUA, utilizando dados de 1980 a 2015. Em azul, temos a prevalência de pessoas vivendo com HIV, e em laranja, a taxa de óbito por Síndrome da Imunodeficiência Adquirida (AIDS).

Figura 4 - Prevalência de pessoas infectadas pelo HIV e óbitos por AIDS a cada mil pessoas nos Estados Unidos da América, no período de 1980 a 2015 / Fonte: Wikimedia (2018, on-line)4.

Podemos observar que a prevalência de HIV aumentou ao longo dos anos nos EUA, e devemos lembrar que esta medida de frequência é ideal para problemas crônicos, como a infecção pelo HIV, em que os casos existentes acumulam-se ao longo dos anos e não apenas são considerados os casos novos. Por isso, ao longo dos anos, somam-se os casos existentes aos novos.

Além disso, devemos levar em consideração os casos em que houve a cura ou o óbito. Nesses, devemos reduzir o numerador, pois não são mais considerados casos existentes (GORDIS, 2009; PEREIRA, 2003). Podemos representar a prevalência utilizando um tanque de água:

A prevalência é o número de casos existentes de uma doença (conteúdo de dentro do tanque), que considera o número de casos novos (que enche o tanque) e os antigos (dentro do tanque), reduzindo do total o número dos casos que evoluíram para a cura (não existem mais, e portanto, saem do tanque) e que levaram ao óbito (também não existem mais e saem do tanque).

Zoom no Conhecimento

A prevalência é útil para avaliar o peso de uma doença na comunidade, e não pode ser considerada uma medida de risco (GORDIS, 2009; FRANCO; PASSOS, 2011; PEREIRA, 2003). Ela é muito utilizada e valiosa para o planejamento de serviços de saúde e como ferramenta sugestiva de fatores etiológicos, pois se trata de uma medida que se refere ao passado, e não a dados novos, como a incidência. Esta sim é considerada uma medida de risco, pois explora a relação entre a exposição a um fator e o risco de desenvolver a doença.

No caso de planejamento em saúde, podemos, por exemplo, estimar o número de pessoas que possuem artrite reumatoide na comunidade e, a partir disso, calcular o número de clínicas necessárias, que tipos de serviços de reabilitação deveremos implantar, quantos profissionais de saúde deverão compor o quadro de servidores e outras medidas. Em relação à sugestão de fatores etiológicos, podemos utilizar a prevalência quando é difícil medir a incidência de uma doença, como no caso da asma, em o momento exato do início da doença é de difícil definição (GORDIS, 2009; FRANCO; PASSOS, 2011).

Os dados para cálculo da prevalência geralmente são obtidos por inquéritos, entrevistas, questionários e até por autorrelato. Por isso, devemos levar em consideração muitos vieses que podem ocorrer como (GORDIS, 2009; PEREIRA, 2003):

Figura 5 – Esquema representativo da prevalência.

Fonte: a autora.

muitas vezes definir quem tem a doença não é uma tarefa fácil. Isso pode ocorrer quando a doença é de difícil diagnóstico, como a asma, a artrite reumatóide ou a neoplasia. Ou ainda, a pessoa pode ter a doença, mas não está ciente que a possui, ou não tem a atenção médica ou a informação. O indivíduo pode ainda não recordar de ter tido o episódio da doença ou a exposição aos fatores investigados. O entrevistador ou pesquisador pode não cadastrar corretamente a informação ou não formular corretamente a pergunta, ou ainda ser tendencioso;

contagens seletivas de certos grupos na população, deixando de adicionar todos os indivíduos que deveriam compor o denominador. Outro erro é o de utilizar os dados populacionais do IBGE de um ano diferente do estudado. Gordis (2009) afirma que todos do denominador devem ter o potencial para entrar no grupo representado no numerador. Como exemplo: em um estudo que avalia a prevalência de câncer de colo uterino, mulheres histerectomizadas (histerectomia é a remoção parcial ou total do útero) não devem compor o denominador, pois não estão sob o risco de câncer de colo uterino. Incluí-las no denominador levaria a taxas incorretas.

as admissões nos hospitais são seletivas em relação às características pessoais, à gravidade da doença, às condições associadas, e às políticas de admissão; os registros hospitalares não são elaborados para pesquisas e podem ser incompletos, ilegíveis ou perdidos, ou ainda muito variados na qualidade do diagnóstico; a população do denominador não é geralmente bem definida.

INCIDÊNCIA

A incidência é uma medida de frequência dinâmica , como um filme, e é prospectiva. Isso significa que as frequências das doenças variam conforme se passa o tempo. Sem contar os casos antigos, ela mede os dados do presente e os novos que surgem prospectivamente (GORDIS, 2009; FRANCO;PASSOS, 2011; PEREIRA, 2003). Um exemplo de prospectivo é quando se inicia um estudo em 2017 e os dados são coletados nesse mesmo ano e nos seguintes, por exemplo até 2020 . Ou ainda, os dados são coletados do passado, mas só se contabilizam os casos novos e não os que persistiram ao longo dos anos do estudo. A incidência de uma doença é definida como o número de casos novos de uma doença ou agravo que ocorrem um período determinado de tempo em uma população que está sob o risco de desenvolver a doença. O cálculo da taxa de incidência se dá pela equação (GORDIS, 2009; FRANCO; PASSOS, 2011; PEREIRA, 2003):

Número de casos novos da doença em um período de tempo, dividido pelo número de pessoas da população sob o risco de desenvolver a doença. o Resultado deve ser multiplicado por 10n

No denominador, devemos utilizar a população exposta ao risco de desenvolver a doença, ou seja, aquelas que já possuem a doença não podem ser contadas para compor o denominador.

A potência de 10 pode ser 100 (%), 1.000, 10.000, 100.000, 1 milhão ou outro número. O fundamental na incidência é contar apenas os casos NOVOS no numerador. A incidência mede a ocorrência de um evento, a identificação de uma pessoa que desenvolve uma doença e que não a apresentava anteriormente. Como é uma medida que avalia a transição do saudável para o doente, dizemos que a incidência é uma medida de risco, diferentemente da prevalência (GORDIS, 2009; FRANCO; PASSOS, 2011; PEREIRA, 2003).

O denominador deve ser composto apenas por mulheres, pois homens não possuem potencial para ter câncer de colo uterino.

O indivíduo do denominador deve ter potencial para ser um numerador (GORDIS, 2009). Tomemos como exemplo a pesquisa da incidência de câncer de colo uterino. Neste caso, o denominador deve ser composto apenas por mulheres, pois os homens não possuem potencial para ter câncer de colo uterino. O mesmo se aplica para a pesquisa de câncer de próstata em homens, na qual não devemos incluir as mulheres no denominador, uma vez que não possuem próstata.

A incidência é muito útil para medir a frequência e a magnitude de problemas agudos (dengue, gripe, infecções parasitárias, alergias). As doenças que os geram têm curta duração e os casos não se mantém por longo período, não havendo uma prevalência significativa ao longo de um ano, por exemplo. Para doenças que ocorrem sazonalmente ou cuja duração dos sintomas é de semanas ou poucos meses, podemos utilizar a incidência como medida de frequência (GORDIS, 2009; PEREIRA, 2003).

Também utilizamos a incidência quando pretendemos avaliar a eficácia de uma vacina (estudos do tipo ensaio clínico). Nestes estudos experimentais, uma população sem a doença é submetida à imunização com a vacina e observa-se, ao longo do tempo (prospectivo), o aparecimento da doença, ou seja, a frequência dos casos novos. Veja o exemplo da figura abaixo:

Figura 6 - Incidência de sarampo (measles) a cada um milhão de habitantes nos Estados Unidos, de 1950 a 2001

Fonte: Wikimedia (2018, on-line)5.

Pensando Juntos

Representação gráfica linear do coeficiente de incidência, número de casos a cada um milhão de pessoas (eixo Y: cases =casos; thousands =milhão) de acordo com os anos (eixo X, de 1950 a 2000). A linha do gráfico representa o número de casos por ano. Entre 1960 e 70, foi introduzida a vacinação contra o sarampo. A partir da linha de tendência, observamos que houve um declínio no número de casos. Vaccine licensed = vacina licenciada.

Observamos que, após a introdução da vacina, houve uma redução significativa dos casos novos de sarampo ao longo dos anos.

Tomemos como exemplo a dengue. A duração dos sintomas da doença é de uma semana, assim o indivíduo é incluído como um caso novo quando se constata que está com a doença., Logo após a cura, esse indivíduo está novamente sob o risco de desenvolver a doença e não é considerado um caso existente (veja a figura do tanque no tópico 2). Portanto, se ele for acometido novamente, ele será um caso novo. Por isso, a medida adequada para doenças de curta duração é a incidência.

Para você compreender melhor, daremos um exemplo hipotético sobre a tuberculose:

Tabela 1 - Tuberculose (TB) - Incidência, prevalência e taxa de óbito por 100.000 habitantes, ano de 2015 e 2016, no município X (dados hipotéticos)

Fonte: a autora.

Aprofundando

Neste exemplo, podemos ver a diferença entre incidência e prevalência. No ano de 2015, na cidade X, tinhamos uma população de 500 mil pessoas, 320 casos novos e 42 casos antigos de tuberculose, totalizando 362 casos existentes. A incidência é calculada apenas com os casos novos de tuberculose (320/499.958, lembre-se que o denominador é a população que está sob o risco de adoecer, e 42 já estavam doentes) a cada 100.000 habitantes.

A prevalência se calcula a partir do total de casos, somando-se os antigos e os novos (362/500.000). Por isso, a prevalência é maior que a incidência. Observamos ainda que no ano de 2016 a incidência foi mais elevada, mas a prevalência manteve-se constante, pois a prevalência ainda leva em consideração os casos curados e os óbitos, e reflete a constância da doença ao longo do tempo.

A escolha da medida de frequência deve ser adequada e determinada pela característica de duração da doença.

A tuberculose geralmente é uma doença crônica com duração maior que seis meses a um ano, na qual a prevalência é a medida de frequência mais utilizada, mas a incidência é uma medida que nos mostra o risco de a doença acometer uma população, enquanto a prevalência não (GORDIS, 2009). Portanto, a escolha da medida de frequência deve ser adequada e determinada pela característica de duração da doença. Para doenças de longa duração, podemos utilizar prevalência e incidência, e para as de curta duração, a ideal e recomendada é a incidência. Todas devem ser calculadas quando se têm os números confiáveis do numerador e do denominador (GORDIS, 2009; FRANCO; PASSOS, 2011).

Em algumas situações, podemos utilizar a relação entre a incidência e prevalência, principalmente naquelas em que as taxas de uma doença não se alteram, ou a taxa de imigração é semelhante a de emigração. Podemos aplicar a seguinte equação (GORDIS, 2009; FRANCO; PASSOS, 2011; PEREIRA, 2003):

Prevalência = incidência x duração da doença

A prevalência de doenças crônicas é mais facilmente estabelecida, quando comparada à incidência, o que se faz por inquéritos transversais. Como regra geral, este é o caminho mais simples: determinar a prevalência e, por uma estimativa da duração da doença, obter-se a incidência. Os cálculos são aproximados, por exigirem como premissa a estabilidade da doença na população (ou seja, incidência constante) (GORDIS, 2009; FRANCO; PASSOS, 2011). Tomemos a taxa de incidência de uma determinada neoplasia maligna, cujo coeficiente de prevalência é de seis casos por 100 mil habitantes e a média de evolução do caso seja de dois anos (entre o diagnóstico e o óbito). Utilizando a equação, temos uma incidência de dois casos novos a cada 100 mil habitantes.

MEDIDAS DE ASSOCIAÇÃO PARA ESTUDOS RETROSPECTIVOS

VOCÊ SABE RESPONDER?

Após a identificação dos principais problemas de saúde de uma população, é preciso perguntar: quais são as causas para que ocorram os óbitos, as doenças, os agravos?

A pesquisa dos fatores de risco ou de proteção que determinam os fenômenos de doença e saúde podem ser realizados por estudos epidemiológicos observacionais ou experimentais.

Brevemente, os observacionais são aqueles em que o pesquisador coleta os dados (retrospectivos ou prospectivos), observa os fenômenos finais e os de exposição e não interfere na saúde ou na doença do indivíduo, enquanto que os experimentais são aqueles em que o pesquisador interfere na saúde do indivíduo, como na testagem de uma novo medicamento, vacina ou método de diagnóstico por exemplo (GORDIS, 2009; FRANCO; PASSOS, 2011; BENSEÑOR; LOTUFO, 2005).

Zoom no Conhecimento

Dentro das pesquisas epidemiológicas, os principais estudos biomédicos utilizados para a identificação de fatores de risco que podem desencadear ou favorecer o aparecimento de doenças são os estudos transversais, caso-controle, coorte e ensaio clínico (GORDIS, 2009; BENSEÑOR; LOTUFO, 2005; FRANCO; PASSOS, 2011). Os estudos observacionais retrospectivos, aqueles que utilizam a prevalência de doenças e seus determinantes, são os mais realizados, e os principais são os transversais e de caso-controle (GORDIS, 2009; BENSEÑOR; LOTUFO, 2005). Esses estudos são retrospectivos, pois utilizam dados do passado (exposição e doença).

Por exemplo: um estudo iniciou em 2017, mas os dados são referentes aos anos de 2000 a 2017 (Figura 6). No âmbito do estudo observacional prospectivo, temos os estudos de coorte (Gordis, 2009; Benseñor e Lotufo, 2005), que utilizam a incidência de doenças e seus determinantes. Como exemplo; um estudo iniciou em 2017 e acompanhou os pacientes até 2030 para obter todos os dados de exposição e doença (Figura 6). Os estudos do tipo ensaio clínico são sempre prospectivos e experimentais (intervém na saúde do indivíduo, novos tratamentos, teste de vacinas e outros) (GORDIS, 2009; BENSEÑOR; LOTUFO, 2005).

Aqui, é importante que você compreenda que quando realizamos estudos retrospectivos (transversais e caso-controle), que utilizam dados antigos e do presente (prevalência), nós devemos utilizar a medida de associação de razão de chances ( Odds ratio ) e razão de prevalência (GORDIS, 2009; BENSEÑOR; LOTUFO, 2005). No caso de realizarmos um estudo prospectivo (coorte e ensaio clínico), devemos utilizar a medida de risco relativo ou outra medida de risco (tópico V) (GORDIS, 2009; BUSTO, 2016; FRANCO; PASSOS, 2011; BENSEÑOR; LOTUFO, 2005).

VOCÊ SABE RESPONDER?

O cálculo e a interpretação dessas medidas permitem responder á pergunta: qual é a associação ou o risco de ser exposto a um fator e desenvolver uma doença? As medidas obtidas nos estudos retrospectivos são estimativas do risco, e não o risco verdadeiro, o qual é referido como o risco relativo (GORDIS, 2009). Portanto, dizemos que, quando calculamos a Odds ratio (razão de chances) ou a razão de prevalência (RP), estamos interpretando a probabilidade ou a chance de um evento ocorrer após a exposição a um fator de risco, não inferindo causalidade, mas sim sugerindo as hipóteses dos fatores de risco, enquanto que quando realizamos os estudos prospectivos, de maior credibilidade e confiabilidade científica, calculamos o real risco (risco relativo, RR) de desenvolver um fenômeno após a exposição a um fator de risco. Estes tipos de estudos inferem causalidade (GORDIS, 2009; FRANCO; PASSOS, 2011; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

Figura 7 - Diagrama de tempo para os estudos prospectivos e retrospectivos iniciados em 2017.

Fonte: a autora.

Mas o que seriam associação e causalidade? Essas duas palavras não são sinônimos. Dois eventos podem estar associados sem que um seja a causa do outro; eles podem também estar etiologicamente ligados. O termo associação tem o significado de relação (ou correlação) estatística entre dois ou mais eventos. Causalidade, relação de causa e efeito entre dois eventos, significa que a presença de um deles contribui para a presença do outro (ALMEIDA FILHO; BARRETO, 2011).

É o que ocorre entre um fator de risco e uma doença. A remoção do fator de risco, por sua vez, diminui a frequência da doença. Exemplo: a falta de higiene das mãos, a presença de pessoas doentes em locais fechados, a falta de imunização pela vacina da gripe são fatores que estão associados à gripe, e o agente viral é a causa da doença. O risco é a probabilidade de que pessoas que estão sem uma doença, mas expostas a certos “fatores de risco” adquiram a doença.

VOCÊ SABE RESPONDER?

Qual é o risco da pessoa não vacinada contrair o vírus influenza e adquirir uma gripe?

A investigação epidemiológica gera resultados que indicam os riscos de que uma pessoa exposta a um determinado desenvolva uma enfermidade ou um outro evento. O risco é uma quantificação da associação entre a exposição a um fator e o surgimento de uma doença (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; BENSEÑOR; LOTUFO, 2005). Por exemplo, qual é o risco de desenvolver uma doença coronariana quando exposto a altos níveis de colesterol? Essa resposta pode ser dada a partir de cálculos matemáticos de risco. Logo, o risco é a probabilidade de ocorrer um evento quando há a exposição a um fator.

No entanto, nem todos as pessoas têm os mesmos riscos. Há pessoas que se expõem ou vivem perigosamente e que possuem maior probabilidade de morrer precocemente. Há outras que não se expõem intensamente, mas que estão sobre o risco de adoecer ou sofrer por algum dano, e não de morrer tão precocemente. No caso da doença coronariana, os coeficientes mais elevados estão nos grupos de pessoas que fumam, mas as pessoas que não fumam também podem ser atingidas, porém com menor probabilidade (MEDRONHO, 2009; PEREIRA, 2003; ROUQUAYROL; ALMEIDA FILHO, 1999; BENSEÑOR; LOTUFO, 2005).

Aprofundando

Um dos estudos de coorte mais famosos e que inspiraram muitas pesquisas foi o estudo de Framingham (EUA), conhecido como Framinghan Heart Study. O estudo iniciou em 1949 para lecionada de aproximadamente 10.000 pessoas daquela faixa etária vivendo em Framingham. Destes, 5.127 não tinham doença cardíaca coronariana quando do primeiro exame e estavam, portanto, em risco de desenvolverem DCC. Essas pessoas foram reexaminadas a cada 2 anos para avaliar evidências de DCC, e todas foram submetidas a eletrocardiograma e exames de sangue (triglicerídeos, colesterol total, glicemia, e outros).

O estudo transcorreu por mais de 30 anos e demonstrou que o risco de desenvolver DCC está associado com a pressão arterial, o colesterol sérico, o hábito de fumar, a intolerância a glicose e a hipertrofia ventricular esquerda Fonte: Lotufo (2008). identificar fatores associados com o risco aumentado de doença cardíaca coronariana (DCC).

Para verificarmos a associação entre um fator de risco e uma doença, podemos utilizar as medidas de risco e de probabilidade de um evento ocorrer após a exposição a um fator de risco. Para os estudos retrospectivos do tipo transversal e de caso-controle, recomendamos o cálculo da razão de chances:

Razão de chances (Odds ratio)

A palavra Odds ratio (OR) vem do inglês odds=pares e ratio= proporção, e é a divisão entre a probabilidade de um evento acontecer quando se está exposto ou não a um fator de risco . É uma estimativa do risco relativo, é a chance, a probabilidade (GORDIS, 2009; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

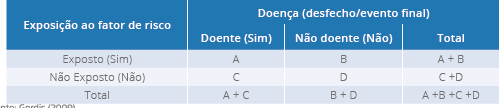
Para compreendermos o cálculo e a interpretação das medidas de OR, razão de prevalência (RP) e risco relativo (RR), é imprescindível construir uma tabela de contingência, também chamada de tabela 2 x 2 (GORDIS, 2009; FRANCO; PASSOS, 2011; BENSEÑOR; LOTUFO, 2005). A sugestão é que você sempre construa a tabela colocando a exposição à esquerda na vertical e o evento final (desfecho: doença, óbito, agravo) à direita na horizontal; veja o exemplo a seguir:

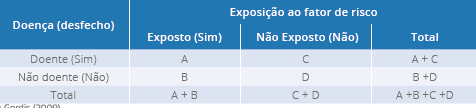
Tabela 2 - Modelo de tabela 2x2 ou de contingência (exposição x desfecho)

Fonte: Gordis (2009).

A outra forma de se construir a tabela é colocando a doença ou desfecho à esquerda, e a exposição à direita na horizontal, como no exemplo:

Tabela 3 - Modelo de tabela 2x2 ou de contigência (desfecho x exposição)

Fonte: Gordis (2009).

Observe que os pares concordantes, as respostas Sim e Sim (A) e Não e Não (B), permanecem no mesmo local em ambas as tabelas, enquanto que os pares que discordam, respostas Não e Sim (C), Sim e Não (D), mudam de posição na tabela. Isso pode confundí-los quando forem aplicar as fórmulas das medidas de associação. Por isso, é sempre importante, entender o cálculo da medida e não só saber aplicar fórmulas.

A razão de chances (OR) é, na verdade, a razão entre o produto dos pares concordantes e o produto dos pares discordantes (GORDIS, 2009; FRANCO; PASSOS, 2011; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

Razão de Chances (OR) = A multiplicado por D, dividido pelo resultado da multiplicação de C e B, logo= A x D/ C x B.

Veja o exemplo de um estudo de caso-controle (dados hipotéticos) em que a exposição ao fumo foi verificada como fator de associação com o câncer de pulmão. Os casos de câncer pulmão são aqueles confirmados por exames e clínica, e os controles são indivíduos que diferem apenas na ausência da doença.

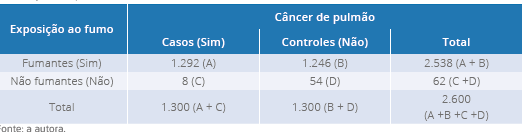
Tabela 4 - Exemplo 1, tabela de contingência de estudo de caso-controle sobre o câncer de pulmão e exposição ao fumo (dados hipotéticos)

Fonte: a autora.

Assim, de 1.300 pessoas com o câncer de pulmão, 1.296 relataram serem fumantes; e de 1.300 controles, 1.246 também eram fumantes. Neste caso, como se trata de um estudo retrospectivo, a medida de OR é a mais apropriada para indicar uma associação entre o fumo e o câncer de pulmão. Logo:

OR= A x D/ C x B= 1.292 x 54/ 1.246 x 8 = 69.768/9.968= 6,99 ≈ 7

A interpretação da OR é que os indivíduos expostos ao risco (fumantes) apresentaram uma probabilidade sete vezes maior de serem atingidos pelo câncer de pulmão do que os não-expostos (não-tabagistas). Existe uma probabilidade sete vezes maior de o evento ocorrer nos expostos em relação a uma vez nos não expostos. Quando a relação é maior que 1, como nesse caso (7), existe o risco de quando exposto ao fator analisado, desenvolver-se a doença.

Quando o resultado de OR, RP e RR forem maior que um (1), existe risco/probabilidade ou chance de o desfecho (doença, óbito o outro evento) ocorrer nos indivíduos expostos ao fator de risco. O resultado quantitativo significa quantas vezes o risco da doença ocorrer no grupo exposto é maior do que no grupo não exposto (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

Veja o mesmo exemplo, mas alocando a exposição e a doença em locais diferentes da tabela 2 x 2:

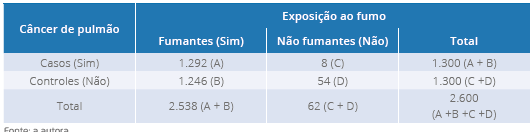
Tabela 5 - Exemplo 2, tabela de contingência de estudo de caso-controle sobre o câncer de pulmão e exposição ao fumo (dados hipotéticos)

Fonte: a autora.

O resultado é o mesmo, no entanto, a tabela de contingência é construída diferente.

Outro exemplo hipotético: um estudo transversal verificou o consumo de carnes gordurosas duas vezes por semana ou mais em indivíduos com dislipidemia (alterações nos níveis de lipídios no sangue). Veja os resultados hipotéticos:

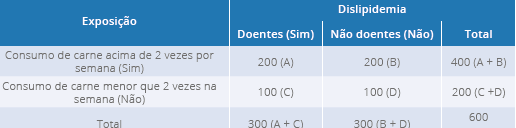
Tabela 6 - Exemplo 2, tabela de contingência de um estudo transversal sobre a dislipidemia e o consumo semanal de carne (dados hipotéticos)

Fonte: a autora.

Logo, OR = (200 x 100)/ (200 x 100)= 20000/20000= 1 (um). Neste caso, não há associação entre o consumo de carne gordurosa, hipoteticamente, em relação às dislipidemias. O consumo de carne gordurosa não interferiu no indivíduo desenvolver essa doença, ou seja, a probabilidade da dislipidemia ocorrer em indivíduos que consomem carne gordurosa mais de duas vezes por semana com aqueles que se alimentam com menor quantidade é a mesma.

Portanto, quando OR, RP e RR forem igual a 1, não há associação entre a exposição ao fator de risco e a ocorrência do desfecho final. A chance de o aparecimento de uma doença é a mesma para o grupo exposto e o não exposto (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

Um outro exemplo hipotético: acadêmicos de medicina realizaram um estudo transversal para verificar se as pessoas que possuíam câncer de pele utilizavam protetor solar (com filtro solar maior ou igual a 15) no rosto e corpo. Observe o resultado:

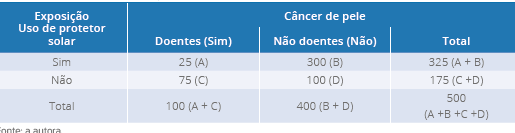
Tabela 7 - Exemplo 3, tabela de contingência de um estudo transversal sobre o câncer de pele e o uso de protetor solar

Fonte: a autora.

Logo, a OR é = (25 x 100)/ (300 x 75) = 2.500/22.500 = 0,11. Neste caso, a OR foi menor que um, ou seja, a chance do evento ocorrer no grupo exposto foi menor que uma vez. Este resultado mostra que o uso do protetor solar não é um fator de risco, mas sim de proteção (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009). Para que os clínicos entendam esse valor menor que um, podemos fazer o seguinte raciocínio:

Se 1 é a chance nula (não há associação), logo 1 – 0,11 (OR) = 0,89 multiplicado por 100 porcento = 89% de chance a menos da doença ocorrer nos indivíduos expostos em relação ao não expostos.

Portanto, quando OR, RP e RR for menor que um, isso indica a presença de um fator de proteção e não de risco. Não devemos jamais descrever as medidas de associação com resultado menor que um desta maneira: a chance de o indivíduo exposto desenvolver a doença é 0,11 vezes maior que no indivíduo não exposto. Você pode observar que não faz sentido a afirmação. Portanto, devemos prestar muita atenção nos resultados de OR, RP e RR, para que se possa interpretá-los de forma correta, evitando a confusão e a descredibilidade do resultado.

Zoom no Conhecimento

Conforme exemplo anterior do câncer de pulmão, podemos também expor diferentemente o resultado de OR e RR acima de 1, neste caso:

Outra forma de DESCREVER para melhor interpretação pelos clínicos:

OR = 7, logo 7 – 1 (fator de não associação) = 6 x 100% = 600% de chance a mais de desenvolver a doença quando exposto a um fator de risco em relação ao não exposto.

Como visto anteriormente, a Epidemiologia tem raízes na Bioestatística e, atualmente, vemos o uso universal de valores de P e a referência “estatisticamente significativo” nos estudos epidemiológicos. Utilizamos o valor de p ou o intervalo de confiança para considerar um resultado significativo ou não. Esses valores são obtidos a partir da aplicação de testes estatísticos de hipóteses, como o de Pearson, o qui-quadrado e outros. O intervalo de confiança é o intervalo de valores do parâmetro analisado, uma faixa ampla que leva em conta o erro aleatório da pesquisa e depende de um nível (usualmente o alfa) que especifique o grau de compatibilidade dos dados com os limites do intervalo. O intervalo de confiança de 95% é usualmente considerado na área da saúde (nível alfa como limite), conhecido como valor de p. Neste caso o valor de p é de 0,05. É fundamental aplicar corretamente a estatística para validar os resultados epidemiológicos. Font e: Rothman, Greenland e Lash (2011).

Razão de prevalência (RP)

A razão de prevalência é outra medida de associação que pode ser utilizada para verificar a probabilidade de o evento acontecer na população. Expressa uma comparação matemática da prevalência entre os grupos de expostos e não-expostos a um determinado fator em estudo. Significa quantas vezes a prevalência é maior ou menor quando existe a exposição a determinado fator (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009). O cálculo de RP é = prevalência da doença nos expostos / prevalência da doença nos não expostos = (A/A+B)/(C/C+D) (GORDIS, 2009). Tomemos o exemplo da tabela 4 (exemplo 1): Logo, a prevalência do câncer de pulmão é de 1.292 em 2.538 pessoas expostas ao fumo, e de 8 casos em 62 pessoas não fumantes.

Assim, RP = (1.292/1.292+ 1.246) / (8/8+54) = (1.292/2.538) / (8/62) = 0,51/0,13 = 3,9 ≈ 4. Portanto, a prevalência de câncer de pulmão é quatro vezes maior em indivíduos fumantes em relação aos não fumantes. Atualmente, observamos que os estudos epidemiológicos retrospectivos têm utilizado mais a medida de OR do que RP para verificar a associação de fatores de risco com doenças e outros eventos. Acredita-se que, como RP tem o mesmo fundamento que o risco relativo, mas não infere causalidade por se tratar de estudo retrospectivo e ser uma medida que estima o risco e não o confirma, OR ainda é a medida mais apropriada e que evita confusão e interpretação inadequada. O resultado de RP > 1, = 1 ou < 1 deve ser interpretado como OR e RR, ou seja, <1 indica fator de proteção, = 1 não há associação, e >1 indica fator de risco (PEREIRA, 2003; ALMEIDA FILHO; BAR- RETO, 2011; GORDIS, 2009; MEDRONHO, 2009; BENSEÑOR; LOTUFO, 2005).

MEDIDAS DE ASSOCIAÇÃO PARA ESTUDOS PROSPECTIVOS

Para os estudos prospectivos , como de coorte e ensaios clínicos, calculamos incidência como medida de frequência e risco relativo (a mais indicada) como medida de associação. Nestes casos, a medida de risco é verdadeira e infere causalidade, ou seja, indica o real fator de risco de uma doença, a causa de uma doença. Esses estudos afirmam as hipóteses levantadas nos estudos retrospectivos . Nesses estudos, o risco pode ser interpretado como (PEREIRA, 2003; GORDIS, 2009; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005):

indica o número de casos novos de uma doença ou outro evento em um determinado período. Utilizando a doença coronariana como exemplo, teríamos 15 óbitos por coronariopatia por ano a cada mil adultos com colesterol sérico elevado, e cinco óbitos a cada mil adultos com níveis baixos. Essa é a forma mais adequada e simples de quantificar o risco, e seu maior significado é quando comparado com resultados obtidos anterior ou posteriormente. Esta comparação é obtida pelo cálculo do risco relativo ou do risco atribuível;

é o cálculo que resulta em quantas vezes o risco de desenvolver uma doença é maior em um grupo comparado a outro grupo. Podemos calcular quantas vezes é o risco de uma pessoa exposta a um fator desenvolver um evento em relação à não exposta. Continuando o exemplo, o risco relativo é calculado pela razão entre as duas taxas de incidência (15 dividido por 5 resultando em 3). O RR indica que o risco de morrer por doença coronariana é três vezes maior em indivíduos com colesterol sérico elevado em relação aqueles que possuem colesterol sérico baixo;

é a diferença entre a incidência do evento em dois grupos, o do exposto a um fator de risco e do não exposto. No exemplo da doença coronariana, o RA é a diferença entre as incidências (15 - 5= 10). Sendo assim, ocorrem 10 óbitos anuais por coronariopatia por mil adultos com colesterol sérico elevado. Seriam os óbitos em excesso.

O RR é a medida de associação mais utilizada atualmente, e expressa uma comparação matemática do risco de adoecer entre grupos de expostos e não-expostos a um determinado fator em estudo (PEREIRA, 2003; ALMEIDA FILHO;; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009; BUSATO, 2016). Logo, a equação do RR é: RR= incidência no grupo exposto (A/A+B) dividido pela incidência no grupo não exposto (C/C+D)

RR= incidência no grupo exposto (A/A+B) dividido pela incidência no grupo não exposto (C/C+D)

Veja o modelo de tabela 2x2 para cálculo do risco relativo:

Tabela 8 - Modelo de tabela para cálculo de risco relativo

Fonte: adaptado de Gordis (2009).

Exemplo: um estudo de coorte (hipotético), selecionou 11.000 pessoas ao longo de 10 anos e observou o número de pessoas que adoeciam por doença cardiovascular e associou com a exposição à diabetes mellitus :

Tabela 9 - Exemplo 1, modelo de um estudo de coorte sobre a doença cardiovascular e a exposição à diabetes mellitus.

Fonte: a autora.

Logo, RR= 6 significa que a incidência de doença cardiovascular é seis vezes maior quando a pessoa possui diabetes mellitus em relação àquelas que não possuem diabetes.

Outro exemplo hipotético: um estudo do tipo ensaio clínico avaliou a eficácia da vacina contra pneumonia e verificou a incidência da doença ao longo de 10 anos após a vacinação. Tomemos os seguintes resultados:

Tabela 10 - Exemplo 2, tabela de contingência de um ensaio clínico para uma vacina contra a pneumonia.

Fonte: a autora.

Neste caso, temos um risco relativo de 0,5. Esse resultado mostra que a vacina teve um efeito protetor contra a pneumonia (1 - 0,5 = 0,5 x 100% = 50%), em que o risco de se desenvolver a pneumonia é 50% menor nos vacinados em relação aos que não receberam a vacina. O resultado menor que 1 é muitas vezes encontrado quando desejamos testar novos medicamentos, vacinas e métodos de diagnóstico de doenças (BENSEÑOR; LOTUFO, 2005).

Aprofundando

Caso, o RR apresente um resultado igual a 1, isso indica que a incidência da doença é a mesma no grupo exposto e não exposto, não havendo diferença, ou ainda que não há associação entre o fator pesquisado e a doença, não podendo considerá-lo fator de risco ou de proteção (PEREIRA, 2003; ALMEIDA FILHO; BARRETO, 2011; GORDIS, 2009; MEDRONHO, 2009; BUSATO, 2016; BENSEÑOR; LOTUFO, 2005).

Resumindo,

Se RR, OR e RP:

= 1 Não há associação

> 1 Risco nos expostos > não expostos (Risco)

< 1 Risco nos expostos < não expostos (proteção)

Novos desafios

Estudante chegamos ao final desta unidade. Esperamos que você tenha compreendido a importância e as aplicações das medidas de frequência e de associação.

Vimos a importância da frequência e distribuição das doenças de acordo com o tempo, pessoa e lugar e utilizamos para isso figuras e tabelas, além das medidas de frequência, prevalência, incidência, seus cálculos e interpretações. Nós utilizamos exemplos hipotéticos para que você possa compreender a aplicação dessas medidas na verificação da situação de saúde das populações e determinar quais são as doenças ou causas de enfermidades que ocorrem com maior frequência nas populações.

Abordamos as medidas de associação e suas aplicações para a identificação de fatores de risco, causas ou ainda fatores de proteção que levam à ocorrência de doenças, óbitos ou outros desfechos em saúde. Destacamos as medidas de odds ratio (proporção dos pares, razão das chances) e a razão de prevalência como medidas de associação para os estudos retrospectivos, aqueles que utilizam dados do passado e presente (prevalência), como os transversais e de caso-controle. Destacamos o risco relativo, utilizado em estudos prospectivos, como os de coorte e o ensaio clínico, que utilizam a incidência dos eventos. Você pode aprender como interpretar o resultado das medidas de associação e a identificar fatores de risco ou de proteção para as doenças.

Como você pode observar, existem muitos tipos de estudos, retrospectivos e prospectivos, que podem ser realizados para verificar a situação de saúde das populações e identificar fatores de risco e de proteção para as doenças.

Espero que tenha tirado máximo proveito desse conteúdo.

REFERÊNCIAS

ALMEIDA FILHO, N. de; BARRETO, M. L. Epidemiologia & saúde: fundamentos, métodos, aplicações. Rio de Janeiro: Guanabara Koogan, 2011, p. 699.

BENSEÑOR, I. M.; LOTUFO, P. A. Epidemiologia: abordagem prática. São Paulo: SARVIER, 2005, p. 303.

BRASIL. Sala de Apoio à Gestão Estratégica. Ministério da Saúde. Disponível em: . Acesso em: 20 jul. 2017.

BUSATO, I. M. S. Epidemiologia e processo saúde-doença. Curitiba: InterSaberes, 2016, p. 244.

FRANCO, L. J.; PASSOS, A. D. C. Fundamentos de Epidemiologia. 2. ed. Barueri: Manole, 2011, p. 424.

GORDIS, L. Epidemiologia. 4. ed. Rio de Janeiro: Revinter, 2009, p. 392.

LOTUFO, P. A. O escore de risco de Framingham para doenças cardiovasculares. Revista Médica, São Paulo, v. 87, n. 4, p. 232-237, 2008.

MEDRONHO, R. de A.; BLOCH, K. V.; LUIZ, R. R.; WERNECK, G. L. Epidemiologia. 2. ed. São Paulo: Atheneu, 2009, p. 685.

PEREIRA, M. G. Epidemiologia: teoria e prática. 6. ed. Rio de Janeiro: Guanabara Koogan, 2003, p. 596.

ROTHMAN, K. J.; GREENLAND, S.; LASH, T. L. Epidemiologia moderna. 3. ed. Porto Alegre: Artmed, 2011, p. 887.

ROUQUAYROL, M. Z.; ALMEIDA FILHO, N. de. Epidemiologia & Saúde. 5. ed. Rio de Janeiro: MEDSI, 1999, p. 600.

UNAIDS. Global prevalence of HIV, 2009. Disponível em: . Acesso em: 20 de julho de 2017.

REFERÊNCIA ON-LINE

Em:https://commons.wikimedia.org/wiki/File:People_living_with_HIV_AIDS_world_map.PNG . Acesso em: 27 fev. 2018.

Em: http://sage.saude.gov.br . Acesso em: 27 fev. 2018.

Em: https://commons.wikimedia.org/wiki/File:HIV_Epidem_2.png . Acesso em: 27 fev. 2018.

Em: https://commons.wikimedia.org/wiki/File:Prevalence_of_HIV_infections_in_the_United_ States_and_total_AIDS_deaths.svg . Acesso em: 27 fev. 2018.

Em: https://commons.wikimedia.org/wiki/File:Measles_incidence-cdc.gif . Acesso em: 27 fev. 2018.